
(本小题10分)如图,ABCD是正方形,O是正方形的中心, PO![]() 底面ABCD,
底面ABCD,
 E是PC的中点。
E是PC的中点。
求证:(1)PA∥平面BDE (2)平面PAC![]() 平面BDE
平面BDE
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:2011-2012学年广东省肇庆市高三数学复习必修2立体几何部分试卷 题型:解答题
(本小题10分)如图,圆锥形封闭容器,高为h,圆锥内水面高为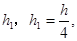 若将圆锥倒置后,圆锥内水面高为
若将圆锥倒置后,圆锥内水面高为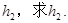
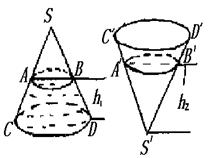
查看答案和解析>>
科目:高中数学 来源:2011年河南省卫辉市高二上学期末理科数学卷 题型:解答题
(本小题10分)
如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长.

查看答案和解析>>
科目:高中数学 来源:2014届福建省高一第一学期期末考试数学 题型:解答题
.(本小题10分)
如图,在四棱锥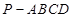 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱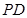 ⊥底面
⊥底面 ,
,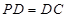 .
.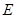 是
是 的中点.(1)证明
的中点.(1)证明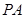 ∥平面
∥平面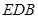 ;(2)证明:
;(2)证明: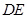 ⊥平面
⊥平面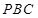 .
.
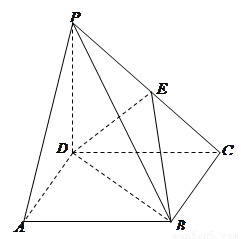
查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市七校高二上学期期中考试数学理卷 题型:解答题
(本小题10分)
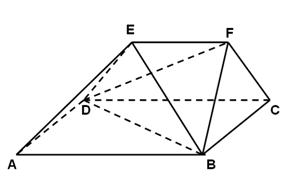
如图,在多面体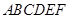 中,四边形
中,四边形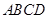 是正方形,
是正方形,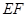 ∥
∥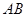 ,
,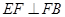 ,
,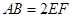 ,
,
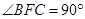 ,
,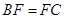 .
.
(1)求二面角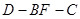 的正切值;
的正切值;
(2)求证:平面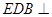 平面
平面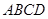 .
.
查看答案和解析>>
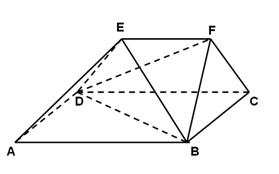
科目:高中数学 来源:2010年浙江省杭州市七校高二上学期期中考试数学文卷 题型:解答题
(本小题10分)
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC.
(1)求证:平面ABFE⊥平面DCFE;
(2)求四面体B—DEF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com