
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{4}$] | B. | (0,$\frac{1}{4}$) | C. | (-$\frac{1}{4}$,0) | D. | [-$\frac{1}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 对某电子元件进行寿命追踪调查,所得情况如频率分布直方图.(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;
对某电子元件进行寿命追踪调查,所得情况如频率分布直方图.(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
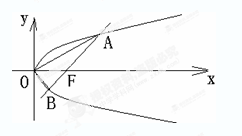 过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 8 | B. | 20+8$\sqrt{2}$ | C. | 16 | D. | 24+8$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com