
| an |
| a1 |
| an |
| 1 |
| 2 |
| an |
| an-1 |
| an |
| π |
| 4n(n-1)θn |
| a1 |
| a1 |
| a2 |
| an |
| a1 |
| d1 |
| d2 |
| dn |
| ODn |
| d1 |
| d2 |
| dn |
| lim |
| n→∞ |
| lim |
| n→∞ |
| a1 |
|
| ||
|
|
| ||
| 2 |
| π |
| 4n(n-1)θn |
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
1-(-
| ||
1-(-
|
| 4 |
| 5 |
| 1 |
| 4 |
1-(-
| ||
1-(-
|
| 8 |
| 5 |
| 1 |
| 4 |
| lim |
| n→∞ |
| 4 |
| 5 |
| lim |
| n→∞ |
| 8 |
| 5 |
| an |
| 1 |
| 2 |
| (xn-1-yn-1)2+(xn-1+yn-1)2 |
| ||
| 2 |
|
| ||
| 2 |
| an-1 |
| a1 |
|
| ||
|
|
| ||
| 2 |
| an |
| ||||
|
|
(xn-1,yn-1)•
| ||||||
|
| ||||||||
|
| ||
| 2 |
| π |
| 4 |
| π |
| 4n(n-1)θn |
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
| a1 |
| a2 |
| 1 |
| 2 |
| 3 |
| 2 |
| a3 |
| 1 |
| 2 |
| a4 |
| 1 |
| 2 |
| 3 |
| 2 |
| a5 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| a1 |
| a5 |
| a9 |
| dn |
| a4n-3 |
| dn |
| 1 |
| 4 |
1-(-
| ||
1-(-
|
| 4 |
| 5 |
| 1 |
| 4 |
1-(-
| ||
1-(-
|
| 8 |
| 5 |
| 1 |
| 4 |
| lim |
| n→∞ |
| 4 |
| 5 |
| lim |
| n→∞ |
| 8 |
| 5 |
| 4 |
| 5 |
| 8 |
| 5 |


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
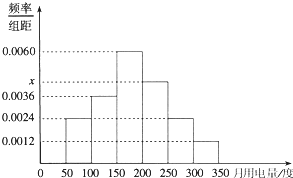 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 22 |
| 4 |
| 32 |
| n+1 |
| n2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
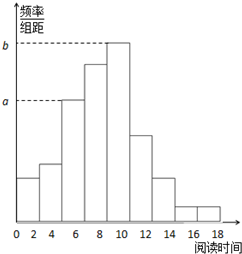 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:| 组号 | 分组 | 频数 |
| 1 | [0,2) | 6 |
| 2 | [2,4) | 8 |
| 3 | [4,6) | 17 |
| 4 | [6,8) | 22 |
| 5 | [8,10) | 25 |
| 6 | [10,12) | 12 |
| 7 | [12,14) | 6 |
| 8 | [14,16) | 2 |
| 9 | [16,18) | 2 |
| 合 计 | 100 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com