
A.1 B.2 C.3 D.4
思路解析:(1)(直接观察法)f(x)=3+![]() ,
,
∵![]() ∈[0,+∞),
∈[0,+∞),
∴f(x)∈[3,+∞),
即函数y=f(x)=3+![]() 的值域是{y|y≥3}.
的值域是{y|y≥3}.
(2)(二次函数法)由4x-x2≥0,得0≤x≤4,在此区间上(4x-x2)max=4,(4x-x2)min=0,
∴函数y=2-![]() 的值域是{y|0≤y≤2}.
的值域是{y|0≤y≤2}.
(3)(部分分式法)把已知函数化为函数y=![]() (x≠2),由此可得y≠1,
(x≠2),由此可得y≠1,
∵x=2时,y=-![]() ,即y≠-
,即y≠-![]() ,
,
∴函数y=![]() 的值域为{y|y≠1且y≠-
的值域为{y|y≠1且y≠-![]() }.
}.
(4)(换元法)设t=![]() ,则x=1-t2,t≥0,代入得y=f(t)=2×(1-t2)+4t=-2t2+4t+2=-2(t-1)2+4,
,则x=1-t2,t≥0,代入得y=f(t)=2×(1-t2)+4t=-2t2+4t+2=-2(t-1)2+4,
∵t≥0,∴y≤4.综上,选D.
答案:D


科目:高中数学 来源: 题型:
| lnx |
| ex |
| x+2 |
查看答案和解析>>
科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
对于函数y=f(x)(x∈D,D是此函数的定义域)若同时满足下列条件:
(Ⅰ)f(x)在D内单调递增或单调递减;
(Ⅱ)存在区间[a,b]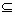 D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.
D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.
(1)求闭函数y=-x3符合条件(Ⅱ)的区间[a,b];
(2)判断函数f(x)=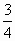 x+
x+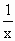 (x∈R+)是否为闭函数?并说明理由;
(x∈R+)是否为闭函数?并说明理由;
(3)若y=k+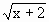 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:第一学期高三期末统一练习数学(文史类) 题型:044
对于函数y=f(x),若同时满足下列条件:
函数y=f(x)在定义域D内是单调递增或单调递减函数;
存在区间[a,b]![]() D,使函数f(x)在[a,b]上的值域为[a,b],则称f(x)是D上的闭函数.
D,使函数f(x)在[a,b]上的值域为[a,b],则称f(x)是D上的闭函数.
求闭函数f(x)=-x3符合条件②的区间[a,b];
判断函数g(x)=![]() 在区间(0,+∞)上是否为闭函数;
在区间(0,+∞)上是否为闭函数;
若函数φ(x)=k+![]() 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:期末题 题型:解答题
 (
( ,D是此函数的定义域),若同时满足下列条件:
,D是此函数的定义域),若同时满足下列条件: 在D内单调递减或单调递增;
在D内单调递减或单调递增;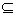 D,使
D,使 在[a,b]上的值域为[a,b];
在[a,b]上的值域为[a,b]; 叫闭函数;
叫闭函数;  符合条件②的区间[a,b];
符合条件②的区间[a,b]; 是否为闭函数?并说明理由;
是否为闭函数?并说明理由; 是闭函数,求实数k的取值范围。
是闭函数,求实数k的取值范围。 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com