
如图,四棱锥 中,
中,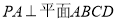 ,底面
,底面 为梯形,
为梯形,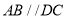 ,
,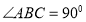 ,且
,且
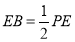 .(10分)
.(10分)

(1)求证: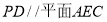 ;
;
(2)求二面角 的余弦值.
的余弦值.
(1)证明见解析;(2)二面角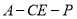 的余弦值为
的余弦值为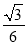 .
.
【解析】
试题分析:(1)连结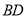 ,交
,交 于点
于点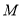 ,连结
,连结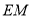 ,由所给条件可得
,由所给条件可得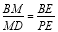 ,即
,即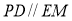 ,则
,则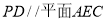 ;(2)以
;(2)以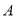 为原点,
为原点,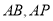 所在直线分别为
所在直线分别为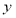 轴、
轴、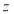 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.
设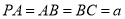 ,则可得
,则可得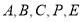 坐标,设
坐标,设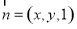 为平面
为平面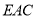 的一个法向量,由
的一个法向量,由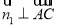
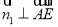 ,可得
,可得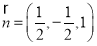 ,同理
,同理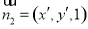 为平面
为平面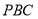 的一个法向量,
的一个法向量,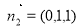 ,
, 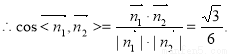 知二面角的余弦值.
知二面角的余弦值.
试题解析:(1)连结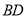 ,交
,交 于点
于点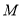 ,连结
,连结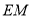 , ∵
, ∵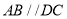 ,
,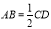 , ∴
, ∴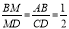
又 ∵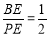 , ∴
, ∴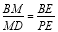 ∴ 在△BPD中,
∴ 在△BPD中, 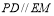
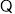
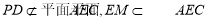 ∴
∴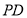 ∥平面
∥平面 ----------------4分
----------------4分
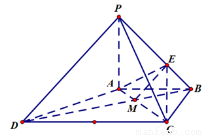
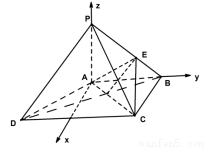
(2)方法一:以 为原点,
为原点,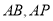 所在直线分别为
所在直线分别为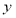 轴、
轴、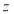 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.
设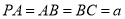 ,则
,则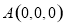 ,
,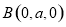 ,
,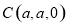 ,
,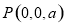 ,
,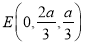 .
.
设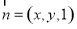 为平面
为平面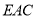 的一个法向量,
的一个法向量,
则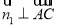 ,
,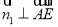 ,∴
,∴ ,
,
解得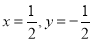 ,∴
,∴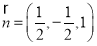 .
.
设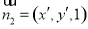 为平面
为平面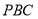 的一个法向量,则
的一个法向量,则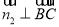 ,
,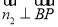 ,
,
又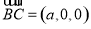 ,
,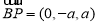 ,∴
,∴ ,
,
解得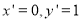 ,∴
,∴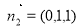
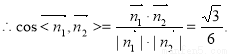
∴二面角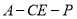 的余弦值为
的余弦值为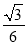 . -------------------10分
. -------------------10分
方法二:在等腰Rt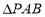 中,取
中,取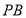 中点
中点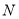 ,连结
,连结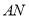 ,则
,则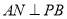
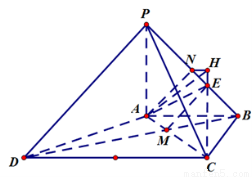
∵面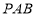 ⊥面
⊥面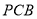 ,面
,面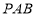
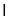 面
面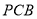 =
=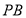 ,∴
,∴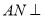 平面
平面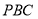 .
.
在平面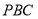 内,过
内,过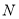 作
作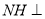 直线
直线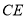 于
于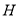 ,连结
,连结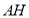 ,由
,由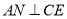 、
、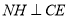 ,
,
得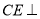 平面
平面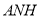 ,故
,故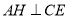 .
.
∴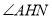 就是二面角
就是二面角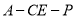 的平面角.
的平面角.
在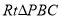 中,设
中,设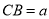 ,
,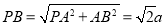 ,
,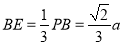 ,
,
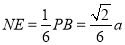 ,
,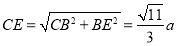 ,
,
由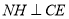 ,
,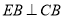 可知:
可知: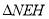 ∽
∽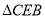 ,
,
∴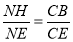 , 代入解得:
, 代入解得: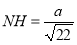 .
.
在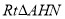 中,
中,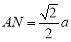 ,
,
∴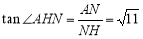 ,
,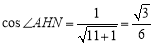 .
.
∴二面角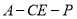 的余弦值为
的余弦值为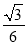 .
.
考点:线面平行的判定定理,二面角,空间向量的坐标运算.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届黑龙江省高二下学期期末文科数学试卷(解析版) 题型:解答题
已知函数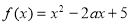 (
(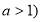 ).
).
(1)若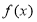 的定义域和值域均是
的定义域和值域均是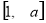 ,求实数
,求实数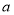 的值;
的值;
(2)若对任意的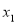 ,
,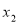
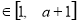 ,总有
,总有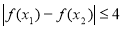 ,求实数
,求实数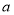 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江大庆铁人中学高二下学期四月月考理科数学试卷(解析版) 题型:选择题
已知随机变量X服从正态分布N(3.1),且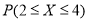 =0.6826,则p(X>4)=( )
=0.6826,则p(X>4)=( )
A.0.1588 B.0.1587 C.0.1586 D.0.1585
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江大庆铁人中学高二下学期四月月考文科数学试卷(解析版) 题型:选择题
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则r=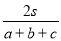 ;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为r,四面体S-ABC的体积为V,则r=( )
;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为r,四面体S-ABC的体积为V,则r=( )
A.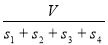 B.
B. 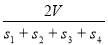 C.
C. 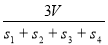 D.
D. 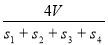
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江哈尔滨第六中学高二下学期期中考试理科数学卷(解析版) 题型:解答题
已知椭圆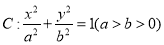 经过点
经过点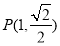 ,且两焦点与短轴的两个端点的连线构成一正方形.(12分)
,且两焦点与短轴的两个端点的连线构成一正方形.(12分)
(1)求椭圆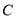 的方程;
的方程;
(2)直线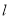 与椭圆
与椭圆 交于
交于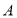 ,
,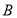 两点,若线段
两点,若线段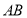 的垂直平分线经过点
的垂直平分线经过点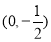 ,求
,求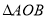
( 为原点)面积的最大值.
为原点)面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江哈尔滨第六中学高二下学期期中考试理科数学卷(解析版) 题型:选择题
已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为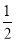 ,则
,则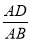 =( )
=( )
A. 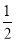 B.
B.  C.
C.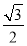 D .
D .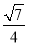
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江哈尔滨第六中学高二下学期期中考试理科数学卷(解析版) 题型:选择题
采用系统抽样方法从960人中抽取32人做问卷调查.为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间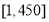 的人做问卷
的人做问卷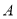 ,编号落入区间
,编号落入区间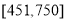 的人做问卷
的人做问卷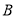 ,其余的人做问卷
,其余的人做问卷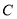 ,则抽到的人中,做问卷
,则抽到的人中,做问卷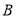 的人数为( )
的人数为( )
A.7 B.9 C.10 D.15
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江哈尔滨第六中学高二下学期期中考试文科数学卷(解析版) 题型:选择题
已知函数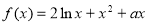 ,若曲线
,若曲线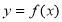 存在与直线
存在与直线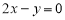 平行的切线,则实数
平行的切线,则实数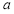 的取值范围是( )
的取值范围是( )
A.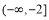 B.
B.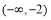 C.
C.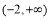 D.
D.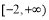
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com