
已知函数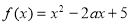 (
(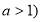 ).
).
(1)若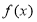 的定义域和值域均是
的定义域和值域均是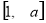 ,求实数
,求实数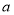 的值;
的值;
(2)若对任意的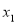 ,
,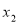
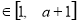 ,总有
,总有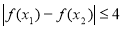 ,求实数
,求实数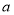 的取值范围.
的取值范围.
(1) 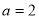 ; (2)
; (2) 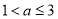 .
.
【解析】
试题分析:(1)首先用配方法求出二次函数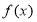 的对称轴为
的对称轴为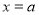 ,由于
,由于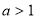 ,知函数
,知函数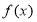 在已知区间
在已知区间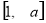 是为减函数,要使函数定义域和值域均为
是为减函数,要使函数定义域和值域均为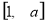 ,必须且只需
,必须且只需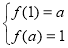 ,从而得到关于a的方程组,解此方程组得实数
,从而得到关于a的方程组,解此方程组得实数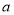 的值;(2)因为对任意的
的值;(2)因为对任意的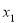 ,
,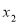
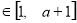 ,总有
,总有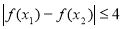 ,等价于:
,等价于: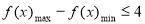 ,所以问题转化为求函数
,所以问题转化为求函数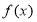 在
在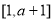 的最大值和最小值;由于二次函数
的最大值和最小值;由于二次函数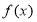 的开口向上,且对称轴为
的开口向上,且对称轴为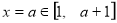 ,所以其最小值一定是
,所以其最小值一定是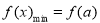 ,而最大值就是两个端点值所对函数值中的较大者,由二次函数的性质可知:等价于比较两个区间的端点谁离对称轴远些;由此只需按
,而最大值就是两个端点值所对函数值中的较大者,由二次函数的性质可知:等价于比较两个区间的端点谁离对称轴远些;由此只需按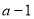 与1的大小进行分类讨论,即可用a的代数式表示出函数
与1的大小进行分类讨论,即可用a的代数式表示出函数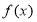 在
在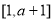 的最大值和最小值,然后代入
的最大值和最小值,然后代入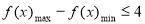 就可求得a的取值范围.
就可求得a的取值范围.
试题解析:(1)∵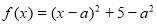 (
(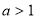 ),
),
∴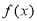 在
在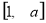 上是减函数,又定义域和值域均为
上是减函数,又定义域和值域均为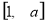 ,∴
,∴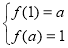 ,
,
即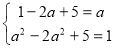 , 解得
, 解得 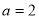 .
.
(2)若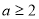 ,又
,又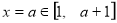 ,且
,且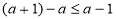 ,
,
∴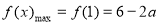 ,
,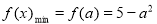 .
.
∵对任意的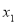 ,
,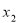
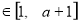 ,总有
,总有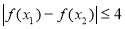 ,
,
∴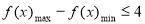 , 即
, 即 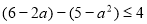 ,解得
,解得 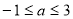 ,
,
又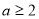 , ∴
, ∴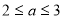 .
.
若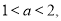
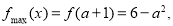
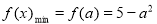 ,
,
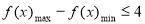 显然成立,
显然成立,
综上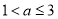 .
.
考点:1.二次函数的单调性与最值;2.分类讨论.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
函数 的图像( ).
的图像( ).
A、 关于原点对称 B、关于主线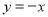 对称
对称
C、 关于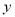 轴对称 D、关于直线
轴对称 D、关于直线 对称
对称
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设函数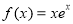 ,则( )
,则( )
A.x=1为 的极大值点
的极大值点
B. x=-1为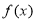 的极大值点
的极大值点
C.x=1为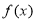 的极小值点
的极小值点
D. x=-1为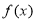 的极小值点
的极小值点
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末理科数学试卷(解析版) 题型:选择题
现有四个函数:①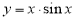 ;②
;② ;③
;③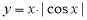 ;④
;④ 的图象(部分)如下:
的图象(部分)如下:

则按照从左到右图象对应的函数序号安排正确的一组是
A.①④②③ B.①④③② C.④①②③ D.③④②①
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末理科数学试卷(解析版) 题型:选择题
命题r:如果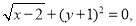 则
则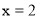 且
且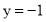 ;若命题r的否命题为p,命题r的否定为q,则
;若命题r的否命题为p,命题r的否定为q,则
A.P真q假 B. P假q真 C. p,q都真 D. p,q都假
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末文科数学试卷(解析版) 题型:填空题
对于定义在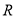 上的函数
上的函数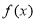 ,有下述四个命题;
,有下述四个命题;
①若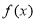 是奇函数,则
是奇函数,则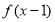 的图像关于点
的图像关于点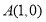 对称;
对称;
②若对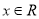 ,有
,有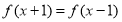 ,则
,则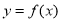 的图像关于直线
的图像关于直线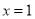 对称;
对称;
③若函数 的图像关于直线
的图像关于直线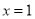 对称,则
对称,则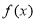 为偶函数;
为偶函数;
④函数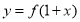 与函数
与函数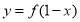 的图像关于直线
的图像关于直线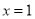 对称。
对称。
其中正确命题为 .
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江大庆铁人中学高二下学期四月月考理科数学试卷(解析版) 题型:填空题
若随机变量X的概率分布密度函数是 (x∈R),则 E(2X1)=_________.
(x∈R),则 E(2X1)=_________.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江哈尔滨第六中学高二下学期期中考试理科数学卷(解析版) 题型:解答题
如图,四棱锥 中,
中,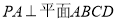 ,底面
,底面 为梯形,
为梯形,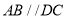 ,
,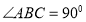 ,且
,且
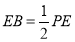 .(10分)
.(10分)

(1)求证: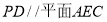 ;
;
(2)求二面角 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com