考点:数列的求和,数列递推式
专题:计算题,等差数列与等比数列
分析:(1)由a
n+12=a
n(a
n+4)+4,可得(a
n+1+a
n+2)(a
n+1-a
n-2)=0,再由a
n>0,得a
n+1-a
n=2,从而可知数列{a
n}为等差数列,易求a
n;
(2)该问题即求数列的周期,由b
n+1=-
可推得b
n+3=b
n;
(3)由(2)知当k∈N
*时,b
3k-2=b
1=1,
b3k-1=b2=-,b
3k=b
3=-2,从而有a
3k-2b
3k-2+a
3k-1b
3k-1+a
3kb
3k=[2(3k-2)-1]×1+[2(3k-1)-1]×(-
)+(2×3k-1)×(-2)=-9k-
,据此可得数列{a
nb
n}的前3n项和S
3n=(a
1b
1+a
2b
2+a
3b
3)+(a
4b
4+a
5b
5+a
6b
6)+…+(a
3n-2b
3n-2+a
3n-1b
3n-1+a
3nb
3n),代入数值可求;
解答:
解:(1)由a
n+12=a
n(a
n+4)+4,得a
n+12=
(an+2)2,
∴(a
n+1+a
n+2)(a
n+1-a
n-2)=0,
由a
n>0,得a
n+1-a
n=2,
∴数列{a
n}为等差数列,且公差为2,
∴{a
n}的通项公式为a
n=2n-1.
(2)b
n+2=-
=-
=-
,
bn+3=-=-
=b
n,
∴当k=3时,对一切n∈N
*有b
n+k=b
n;
(3)
b2=-=-,
b3=-=-2,
由(2)知当k∈N
*时,b
3k-2=b
1=1,
b3k-1=b2=-,b
3k=b
3=-2,
∴a
3k-2b
3k-2+a
3k-1b
3k-1+a
3kb
3k=[2(3k-2)-1]×1+[2(3k-1)-1]×(-
)+(2×3k-1)×(-2)=-9k-
,
∴数列{a
nb
n}的前3n项和
S
3n=(a
1b
1+a
2b
2+a
3b
3)+(a
4b
4+a
5b
5+a
6b
6)+…+(a
3n-2b
3n-2+a
3n-1b
3n-1+a
3nb
3n)
=-9(1+2+…+9)-
n=
-n2-6n.
点评:本题考查由数列递推式求数列通项、数列求和及数列的性质等知识,考查学生运算求解能力.



 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案 已知函数y=2sin(2x+
已知函数y=2sin(2x+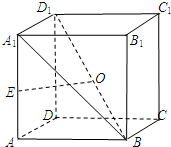 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点.