Question

5．已知AB⊥BC，BC⊥CD，AB=BC=CD，异面直线AB与CD所成的角为$\frac{π}{3}$，则AD与BC所成的角为$\frac{π}{4}$或$\frac{π}{3}$．

Answer 1

分析 作出?ABCE，则∠ECD=$\frac{π}{3}$或$∠ECD=\frac{2π}{3}$，直线AE与AD所成的角∠EAD就是直线BC与AD所成的角，由此利用勾股定理和余弦定理能求出AD与BC所成的角．

解答 解：∵AB⊥BC，BC⊥CD，AB=BC=CD，异面直线AB与CD所成的角为$\frac{π}{3}$，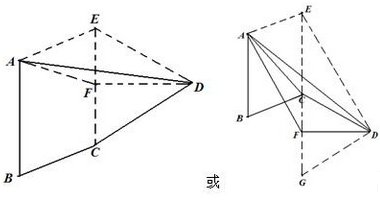
∴如图，作出?ABCE，
则∠ECD=$\frac{π}{3}$或$∠ECD=\frac{2π}{3}$，
直线AE与AD所成的角∠EAD就是直线BC与AD所成的角，
∵AB⊥BC，BC⊥CD，BC∥AE，AB∥EC，
∴AE⊥CD，AE⊥EC，
∵CD∩EC=C，∴AE⊥平面CDE，
设AB=BC=CD=1，则AE=BC=1，
∴当∠ECD=$\frac{π}{3}$时，DE=1，AD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$，
∠EAD=$\frac{π}{4}$，
当$∠ECD=\frac{2π}{3}$时，DE=$\sqrt{1+1-2×1×1×120°}$=$\sqrt{3}$，$AD=\sqrt{1+3}$=2．
∠EAD=$\frac{π}{3}$．
∴AD与BC所成的角为$\frac{π}{4}$或$\frac{π}{3}$．
故答案为：$\frac{π}{4}$或$\frac{π}{3}$．

点评 本题考查两条直线所成角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．