
设数列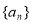 的前
的前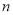 项和为
项和为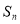 ,已知
,已知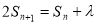 (
(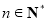 ,
,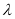 为常数),
为常数),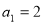 ,
,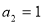 ,(1)求数列
,(1)求数列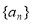 的通项公式;(2)求所有满足等式
的通项公式;(2)求所有满足等式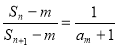 成立的正整数
成立的正整数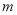 ,
,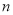 .
.
(1)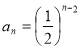 (
(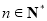 );(2)
);(2)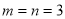 .
.
【解析】
试题分析:(1)由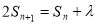 取n=1,及
取n=1,及 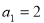 ,
, ,可求得
,可求得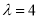 ,再由
,再由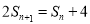 构造两个关系相减求得
构造两个关系相减求得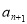 与
与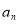 关系,进而知道
关系,进而知道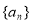 为等比数列,从而可求得通项公式;(2)由(1),得
为等比数列,从而可求得通项公式;(2)由(1),得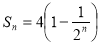 ,代入
,代入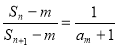 ,同时注意变形技巧,易得n与m的关系,注意到
,同时注意变形技巧,易得n与m的关系,注意到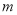 ,
,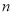 为正整数,以m为分类标准进行讨论,进而求得n与m的值.
为正整数,以m为分类标准进行讨论,进而求得n与m的值.
试题解析:(1)由题意,得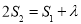 ,求得
,求得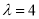 .所以,
.所以,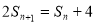 ①
①
当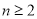 时,
时,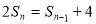 ②
②
①-②,得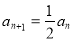 (
(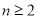 ),又
),又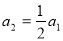 ,所以数列
,所以数列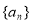 是首项为
是首项为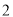 ,公比为
,公比为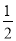 的等比数列,
的等比数列,
故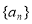 的通项公式为
的通项公式为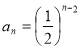 (
(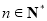 ).
).
(2)由(1),得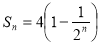 ,由
,由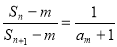 ,两边倒数,且有
,两边倒数,且有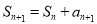 ,因此得
,因此得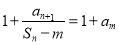 ,化简得
,化简得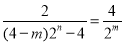 ,即
,即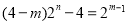 ,即
,即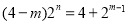 .(*)因为
.(*)因为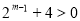 ,所以
,所以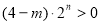 ,所以
,所以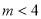 ,因为
,因为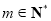 ,所以
,所以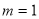 或
或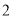 或
或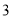 .
.
当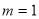 时,由(*)得
时,由(*)得 ,所以无正整数解;
,所以无正整数解;
当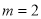 时,由(*)得
时,由(*)得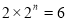 ,所以无正整数解;
,所以无正整数解;
当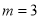 时,由(*)得
时,由(*)得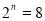 ,所以
,所以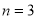 .综上可知,存在符合条件的正整数
.综上可知,存在符合条件的正整数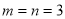 .
.
考点:1,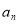 与
与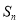 的关系:
的关系: ;2,等比数列通项公式,前n项和公式;3,分类讨论思想.
;2,等比数列通项公式,前n项和公式;3,分类讨论思想.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2016届江苏省高一下学期期中考试数学试卷(解析版) 题型:填空题
已知等差数列{an}的前n项和为Sn=(a+1)n2+a,某三角形三边之比为a2∶a3∶a4,则该三角形的最大角为________.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高一下学期学情分析考试数学试卷(解析版) 题型:填空题
在直三棱柱ABC-A1B1C1中,AB=BC=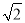 ,B B1=2,∠ABC=90°,E、F分别为A A1,C1 B1的中点,沿棱柱表面,从E到F的最短路径的长为 .
,B B1=2,∠ABC=90°,E、F分别为A A1,C1 B1的中点,沿棱柱表面,从E到F的最短路径的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com