
分析 (Ⅰ)由离心率求得a和c的关系,进而根据c2=a2-b2求得a和b的关系,进而根据$\frac{1}{2}$×2a×2b=4求得a和b,则椭圆的方程可得.
(Ⅱ)(i)由(1)可求得A点的坐标,设出点B的坐标和直线l的斜率,表示出直线l的方程与椭圆方程联立,消去y,由韦达定理求得点B的横坐标的表达式,进而利用直线方程求得其纵坐标表达式,表示出|AB|进而求得k,则直线的斜率可得.
(ii)设线段AB的中点为M,由(i)可表示M的坐标,看当k=0时点B的坐标是(2,0),线段AB的垂直平分线为y轴,进而根据$\overrightarrow{QA}•\overrightarrow{QB}=4$求得y0;当k≠0时,可表示出线段AB的垂直平分线方程,令x=0得到y0的表达式根据$\overrightarrow{QA}•\overrightarrow{QB}=4$求得y0;综合答案可得.
解答 解:(Ⅰ)由e=$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,得3a2=4c2.
再由c2=a2-b2,解得a=2b,
由题意可知$\frac{1}{2}×2a×2b=4$,即ab=2,
解方程组$\left\{\begin{array}{l}a=2b\\ ab=2\end{array}\right.$,
得a=2,b=1.
所以椭圆的方程为$\frac{x^2}{4}+{y^2}=1$.…(3分)
(Ⅱ)(i)解:由(Ⅰ)可知点A的坐标是(-2,0).设点B的坐标为(x1,y1),直线l的斜率为k.
则直线l的方程为y=k(x+2).
于是A、B两点的坐标满足方程组$\left\{\begin{array}{l}y=k(x+2)\\ \frac{x^2}{4}+{y^2}=1.\end{array}\right.$消去y并整理,
得(1+4k2)x2+16k2x+(16k2-4)=0.
由$-2{x_1}=\frac{{16{k^2}-4}}{{1+4{k^2}}}$,得${x_1}=\frac{{2-8{k^2}}}{{1+4{k^2}}}$.从而${y_1}=\frac{4k}{{1+4{k^2}}}$.
所以$|AB|=\sqrt{{{({-2-\frac{{2-8{k^2}}}{{1+4{k^2}}}})}^2}+{{({\frac{4k}{{1+4{k^2}}}})}^2}}=\frac{{4\sqrt{1+{k^2}}}}{{1+4{k^2}}}$.
由$|AB|=\frac{{4\sqrt{2}}}{5}$,得$\frac{{4\sqrt{1+{k^2}}}}{{1+4{k^2}}}=\frac{{4\sqrt{2}}}{5}$.整理得32k4-9k2-23=0,
即(k2-1)(32k2+23)=0,解得k=±1.
所以直线l的倾斜角为$\frac{π}{4}$或$\frac{3π}{4}$.…(7分)
(ii)解:设线段AB的中点为M,由(i)得到M的坐标为$({-\frac{{8{k^2}}}{{1+4{k^2}}},\frac{2k}{{1+4{k^2}}}})$.
以下分两种情况:(1)当k=0时,点B的坐标是(2,0),线段AB的垂直平分线为y轴,
于是$\overrightarrow{QA}=({-2,-{y_0}}),\overrightarrow{QB}=({2,-{y_0}})$.
由$\overrightarrow{QA}•\overrightarrow{QB}=4$,得${y_0}=±2\sqrt{2}$; …(9分)
(2)当k≠0时,线段AB的垂直平分线方程为$y-\frac{2k}{{1+4{k^2}}}=-\frac{1}{k}({x+\frac{{8{k^2}}}{{1+4{k^2}}}})$,
令x=0,解得${y_0}=-\frac{6k}{{1+4{k^2}}}$,
由$\overrightarrow{QA}=({-2,-{y_0}})$,$\overrightarrow{QB}=({{x_1},{y_1}-{y_0}})$,$\overrightarrow{QA}•\overrightarrow{QB}=-2{x_1}-{y_0}({{y_1}-{y_0}})=\frac{{-2({2-8{k^2}})}}{{1+4{k^2}}}+\frac{6k}{{1+4{k^2}}}({\frac{4k}{{1+4{k^2}}}+\frac{6k}{{1+4{k^2}}}})$=$\frac{{4({16{k^4}+15{k^2}-1})}}{{{{({1+4{k^2}})}^2}}}=4$,
整理得7k2=2.
故$k=±\frac{{\sqrt{14}}}{7}$.
所以${y_0}=±\frac{{2\sqrt{14}}}{5}$.
综上,${y_0}=±2\sqrt{2}$或 ${y_0}=±\frac{{2\sqrt{14}}}{5}$.…(12分).
点评 本题主要考查椭圆的标准方程和几何性质、直线的方程、两点间的距离公式、直线的倾斜角、平面向量等基础知识,考查用代数方法研究圆锥曲线的性质及数形结合的思想,考查综合分析与运算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
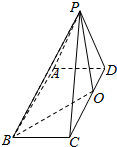 已知点P为矩形ABCD所在平面外一点,AB=3,BC=2,平面PAB∩平面PCD=l.
已知点P为矩形ABCD所在平面外一点,AB=3,BC=2,平面PAB∩平面PCD=l.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2}$x2 | B. | y=lnx | C. | y=$\frac{2}{x}$ | D. | y=-$\frac{1}{3}$x3-2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com