
分析 (Ⅰ)利用导数判断函数的单调性,注意对a分类讨论;
(Ⅱ)利用导数判断函数的极值,注意a的讨论及利用换元法转化为求函数最值问题解决;
(Ⅲ)由均值不等式,可得$\sqrt{x+1}$<$\frac{x}{2}$+1,构造函数k(x)=ln(x+1)-x,可得ln(x+1)<x,从而当x>0时,f(x)<$\frac{3}{2}$x,记h(x)=(x+6)f(x)-9x,可证h(x)在(0,2)内单调递减,从而h(x)<0,故问题得证.
解答 解:(Ⅰ)∵f(x)=ln(1+ax)-$\frac{2x}{x+2}$.
∴f′(x)=$\frac{a}{1+ax}$-$\frac{4}{{(x+2)}^{2}}$=$\frac{{ax}^{2}-4(1-a)}{(1+ax{)(x+2)}^{2}}$,
∵(1+ax)(x+2)2>0,∴当1-a≤0时,即a≥1时,f′(x)≥0恒成立,则函数f(x)在(0,+∞)单调递增,
当0<a≤1时,由f′(x)=0得x=±$\frac{2\sqrt{a(1-a)}}{a}$,则函数f(x)在(0,$\frac{2\sqrt{a(1-a)}}{a}$)单调递减,在($\frac{2\sqrt{a(1-a)}}{a}$,+∞)单调递增.
(Ⅱ)由(Ⅰ)知,当a≥1时,f′(x)≥0,此时f(x)不存在极值点.
因此要使f(x)存在两个极值点x1,x2,则必有0<a<1,又f(x)的极值点值可能是x1=$\frac{2\sqrt{a(1-a)}}{a}$,x2=-$\frac{2\sqrt{a(1-a)}}{a}$
且由f(x)的定义域可知x>-$\frac{1}{a}$且x≠-2,
∴-$\frac{2\sqrt{a(1-a)}}{a}$>-$\frac{1}{a}$且-$\frac{2\sqrt{a(1-a)}}{a}$≠-2,解得a≠$\frac{1}{2}$,
则x1,x2分别为函数f(x)的极小值点和极大值点,
∴f(x1)+f(x2)
=ln[1+ax1]-$\frac{{2x}_{1}}{{x}_{1}+2}$+ln(1+ax2)-$\frac{{2x}_{2}}{{x}_{2}+2}$
=ln[1+a(x1+x2)+a2x1x2]-$\frac{{{4x}_{1}x}_{2}+4{(x}_{1}{+x}_{2})}{{{x}_{1}x}_{2}+2({{x}_{1}+x}_{2})+4}$
=ln(2a-1)2-$\frac{4(a-1)}{2a-1}$=ln(2a-1)2+$\frac{2}{2a-1}$-2.
令2a-1=x,由0<a<1且a≠$\frac{1}{2}$得,
当0<a<$\frac{1}{2}$时,-1<x<0;当$\frac{1}{2}$<a<1时,0<x<1.
令g(x)=lnx2+$\frac{2}{x}$-2.
i)当-1<x<0时,g(x)=2ln(-x)+$\frac{2}{x}$-2,
∴g′(x)=$\frac{2}{x}$-$\frac{2}{{x}^{2}}$=$\frac{2x-2}{{x}^{2}}$<0,
故g(x)在(-1,0)上单调递减,g(x)<g(-1)=-4<0,
∴当0<a<$\frac{1}{2}$时,f(x1)+f(x2)<0;
(ii)当0<x<1.g(x)=2lnx+$\frac{2}{x}$-2,g′(x)=$\frac{2}{x}$-$\frac{2}{{x}^{2}}$=$\frac{2x-2}{{x}^{2}}$<0,
故g(x)在(0,1)上单调递减,g(x)>g(1)=0,
∴当$\frac{1}{2}$<a<1时,f(x1)+f(x2)>0;
综上所述,a的取值范围是($\frac{1}{2}$,1).
(Ⅲ)证明:h(x)+$\sqrt{x+1}$-1=ln(x+1)+$\sqrt{x+1}$-1
由均值不等式,当x>0时,2$\sqrt{(x+1)•1}$<x+1+1=x+2,
∴$\sqrt{x+1}$<$\frac{x}{2}$+1①
令k(x)=ln(x+1)-x,则k(0)=0,k′(x)=$\frac{1}{x+1}$-1=$\frac{-x}{x+1}$<0,∴k(x)<0
∴ln(x+1)<x,②
由①②得,当x>0时,f(x)<$\frac{3}{2}$x
记h(x)=(x+6)f(x)-9x,则当0<x<2时,h′(x)=f(x)+(x+6)f′(x)-9
<$\frac{3}{2}$x+(x+6)($\frac{1}{x+1}$+$\frac{1}{2\sqrt{x+1}}$)-9<$\frac{1}{2(x+1)}$[3x(x+1)+(x+6)(3+$\frac{x}{2}$)-18(x+1)]
=$\frac{x}{4(x+1)}$(7x-18)<0
∴h(x)在(0,2)内单调递减,又h(0)=0,∴h(x)<0
∴当0<x<2时,f(x)<$\frac{9x}{x+6}$.
点评 本题考查导数知识的运用,考查导数的几何意义,考查构造法的运用,考查不等式的证明,正确构造函数是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
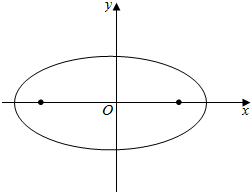 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率 e=$\frac{4}{5}$,且经过点(0,3),左右焦点分别为F1,F2,
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率 e=$\frac{4}{5}$,且经过点(0,3),左右焦点分别为F1,F2,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | (1,3] | C. | [2,+∞) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
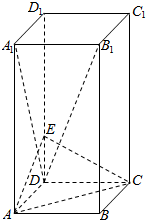 如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点,且满足B1D⊥平面ACE.
如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点,且满足B1D⊥平面ACE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
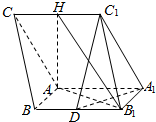 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥侧面ABB1A1,AC=AA1=$\sqrt{2}$AB,∠AA1C1=60°.AB⊥AA1,H为棱CC1的中点,D为BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥侧面ABB1A1,AC=AA1=$\sqrt{2}$AB,∠AA1C1=60°.AB⊥AA1,H为棱CC1的中点,D为BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com