
【题目】已知椭圆C: ![]() (a>b>0)过点(1,
(a>b>0)过点(1, ![]() ),离心率为
),离心率为 ![]() ,过椭圆右顶点A的两条斜率乘积为﹣
,过椭圆右顶点A的两条斜率乘积为﹣ ![]() 的直线分别交椭圆C于M,N两点.
的直线分别交椭圆C于M,N两点.
(1)求椭圆C的标准方程;
(2)直线MN是否过定点D?若过定点D,求出点D的坐标;若不过,请说明理由.
【答案】
(1)解:由已知 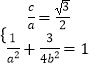 ,∴a=2,b=1,
,∴a=2,b=1,
∴椭圆C的标准方程为 ![]() ;
;
(2)解:直线MN过定点D(0,0).
证明如下:由题意,A(2,0),直线AM和直线AN的斜率存在且不为0,
设AM的方程为y=k(x﹣2),代入椭圆方程得(1+4k2)x2﹣16k2x+16k2﹣4=0
∴2xM= ![]() ,
,
∴xM= ![]() ,
,
∴yM=k(xM﹣2)= ![]() ,
,
∴M( ![]() ,
, ![]() ),
),
∵椭圆右顶点A的两条斜率乘积为﹣ ![]() 的直线分别交椭圆C于M,N两点,
的直线分别交椭圆C于M,N两点,
∴设直线AN的方程为y=﹣ ![]() (x﹣2),
(x﹣2),
同理可得N( ![]() ,
, ![]() ),
),
xM≠xN,即k ![]() 时,kMN=
时,kMN= ![]() ,
,
∴直线MN的方程为y﹣ ![]() =
= ![]() (x﹣
(x﹣ ![]() ),即y=
),即y= ![]() x,
x,
∴直线MN过定点D(0,0).
xM=xN,即k= ![]() 时,直线MN过定点D(0,0).
时,直线MN过定点D(0,0).
综上所述,直线MN过定点D(0,0)
【解析】(1)由椭圆C: ![]() (a>b>0)过点(1,
(a>b>0)过点(1, ![]() ),离心率为
),离心率为 ![]() ,建立方程,求出a,b,即可求椭圆C的标准方程;(2)设AM、AN的方程,代入椭圆方程,求出M,N的坐标,进而可得MN的方程,即可得出结论.
,建立方程,求出a,b,即可求椭圆C的标准方程;(2)设AM、AN的方程,代入椭圆方程,求出M,N的坐标,进而可得MN的方程,即可得出结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一个盒子装有六张卡片,上面分别写着如下六个定义域为![]() 的函数:
的函数: ![]()
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市出租车收费标准如下:①起步价3km(含3km)为10元;②超过3km以外的路程按2元/km收费;③不足1km按1km计费.
(1)试写出收费y元与x(km)(0<x≤5)之间的函数关系式;
(2)若某人乘出租车花了24元钱,求此人乘车里程xkm的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() ,焦点
,焦点![]() ,
, ![]() 为坐标原点,直线
为坐标原点,直线![]() (不垂直
(不垂直![]() 轴)过点
轴)过点![]() 且与抛物线
且与抛物线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若![]() 为线段
为线段![]() 的中点,射线
的中点,射线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z的实部和虚部都是整数,
(1)若复数z为纯虚数,且|z﹣1|=|﹣1+i|,求复数z;
(2)若复数z满足z+ ![]() 是实数,且1<z+
是实数,且1<z+ ![]() ≤6,求复数z.
≤6,求复数z.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人进行羽毛球练习赛,其中两人比赛另一个人当裁判,设每周比赛结束时,负的一方在下一局当裁判,假设每局比赛中甲胜乙的概率为![]() ,甲胜丙,乙胜丙的概率都是
,甲胜丙,乙胜丙的概率都是![]() ,各局的比赛相互独立,第一局甲当裁判.
,各局的比赛相互独立,第一局甲当裁判.
(1)求第三局甲当裁判的概率;
(2)记前四次中乙当裁判的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com