练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f（x）=x2+（2a-1）x+1为偶函数，则实数a的值为
     
    ．
    考点：二次函数的性质
    专题：函数的性质及应用
    分析：由函数的对称性对称2a-1=0，解出a的值即可．
    解答： 解：∵函数f（x）的定义域关于原点对称，
    而f（-x）=x2-（2a-1）x+1=f（x）=x2+（2a-1）x+1，
    ∴2a-1=0，a=
    1
    2
    ，
    故答案为：
    1
    2
    点评：本题考查了二次函数的性质，考查函数的奇偶性，是一道基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    数列{an}，a1=1，an=2n+an-1（n≥2），an=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求方程
    		13-
    		13+x
    =x的实数解．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

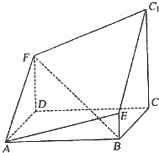    如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的，其中AB=4，BC=2，CC1=3，BE=1
    （Ⅰ）求BF的长；
    （Ⅱ）求面AEC1F与底面ABCD所成二面角的余弦值
    （Ⅲ）求点C到平面AEC1F的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{an}的前n项和为Sn，S3=6a1，且对n∈N*，点（n，an）恒在直线f（x）=2x+k上，其中k为常数．
    （1）求数列{an}的通项公式；
    （2）记Tn=
    1
    S1
    +
    1
    S2
    +
    1
    S3
    +…+
    1
    Sn
    ，求T20的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=x-4
    		x
    +m，当0≤x≤9时，f（x）≥1恒成立，则实数m的取值范围为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    分析说明下列对应是否为A到B的函数：A=[0，2]，B=[0，4]，f取x和x2中的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    应用函数单调性定义证明：函数f（x）=x+
    4
    x
    在区间（0，2）上是减函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

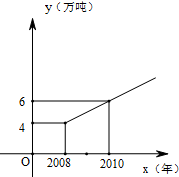    某市实施“限塑令”后，2008年大约减少塑料消耗约4万吨．调查结果分析显示，从2008年开始，五年内该市因实施“限塑令”而减少的塑料消耗量y（万吨）随着时间x（年）逐年成直线上升，y与x之间的关系如图所示．
    （1）求y与x之间的关系式；
    （2）请你估计，该市2011年因实施“限塑令”而减少的塑料消耗量为多少？

    查看答案和解析>>

    同步练习册答案