
���� ��1����A��ʾ�¼���ý���ѡ��5�Ÿ��֡����¼�B��ʾ��ý����ѡ��5�Ÿ��֡���ý���ѡ��5����ý����δѡ��5�Ÿ��ֵĸ���P��A$\overline{B}$��=P��A��P��$\overline{B}$�����ɴ�����������
��2���¼�C��ʾ��ý����ѡ��5�Ÿ��֡���$P��C��=\frac{C_5^2}{C_6^3}=\frac{1}{2}$��X���ܵ�ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�X��������
��� �⣺��1����A��ʾ�¼���ý���ѡ��5�Ÿ��֡����¼�B��ʾ��ý����ѡ��5�Ÿ��֡���
��$P��A��=\frac{C_4^1}{C_5^2}=\frac{2}{5}��P��B��=\frac{C_4^2}{C_5^3}=\frac{3}{5}$��
��ý���ѡ��5����ý����δѡ��5�Ÿ��ֵĸ��ʣ�
P��A$\overline{B}$��=P��A��P��$\overline{B}$��=$\frac{2}{5}��$��1-$\frac{3}{5}$��=$\frac{4}{25}$��
��2���¼�C��ʾ��ý����ѡ��5�Ÿ��֡���$P��C��=\frac{C_5^2}{C_6^3}=\frac{1}{2}$��
��X���ܵ�ȡֵΪ0��1��2��3��
��P��X=0��=P��$\overline{A}\overline{B}\overline{C}$��=��1-$\frac{2}{5}$����1-$\frac{3}{5}$����1-$\frac{1}{2}$��=$\frac{3}{25}$��
P��X=1��=P��A$\overline{B}\overline{C}$��+P��$\overline{A}B\overline{C}$��+P��$\overline{A}\overline{B}C$��
=$\frac{2}{5}����1-\frac{3}{5}������1-\frac{1}{2}��$+��1-$\frac{2}{5}$����$\frac{3}{5}$����1-$\frac{1}{2}$��+$\frac{3}{5}��\frac{2}{5}��\frac{1}{2}$=$\frac{19}{50}$��
P��X=2��=P��AB$\overline{C}$��+P��$A\overline{B}C$��+P��$\overline{A}BC$��=$\frac{2}{5}��\frac{3}{5}��\frac{1}{2}+\frac{2}{5}��\frac{2}{5}��\frac{1}{2}+\frac{3}{5}��\frac{3}{5}��\frac{1}{2}$=$\frac{19}{50}$��
$P��X=3��=P��ABC��=\frac{2}{5}��\frac{3}{5}��\frac{1}{2}=\frac{3}{25}$��
����X�ķֲ���Ϊ
| X | 0 | 1 | 2 | 3 |
| P | $\frac{3}{25}$ | $\frac{19}{50}$ | $\frac{19}{50}$ | $\frac{3}{25}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��м���ѧ���������漰��ƽ�����������ɢ����������ķֲ��м���ѧ������֪ʶ�㣬����������֤����������������������ݴ������������黯����ת��˼�룬���е��⣮


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
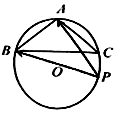 ��ͼ���ڡ�A BC�У����ڽ� A��B��C�ĶԱ߷ֱ�Ϊa��b��c����a2=b2+c2+bc��$a=\sqrt{3}$��SΪ��A BC�������Բ O�ǡ�A BC�����Բ��P��Բ O��һ���㣬
��ͼ���ڡ�A BC�У����ڽ� A��B��C�ĶԱ߷ֱ�Ϊa��b��c����a2=b2+c2+bc��$a=\sqrt{3}$��SΪ��A BC�������Բ O�ǡ�A BC�����Բ��P��Բ O��һ���㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=sinx | B�� | y=sin2|x| | C�� | y=-cos2x | D�� | y=cos2x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
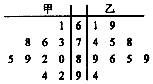 �ס�����λͬѧ�μ���ѧ������ѵ����ѵ�ڼ乲�μ���10��ģ�⿼�ԣ����ݿ��Գɼ����õ�����ͼ��ʾ�ľ�Ҷͼ���涨ģ�⿼�Գɼ�������81��Ϊ����ȴΣ�
�ס�����λͬѧ�μ���ѧ������ѵ����ѵ�ڼ乲�μ���10��ģ�⿼�ԣ����ݿ��Գɼ����õ�����ͼ��ʾ�ľ�Ҷͼ���涨ģ�⿼�Գɼ�������81��Ϊ����ȴΣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
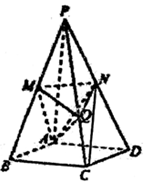 ��ͼ��������P-ABCD�У������DZ߳�Ϊ2$\sqrt{3}$�����Σ��ҡ�BAD=120�㣬��PA��ƽ��ABCD��PA=2$\sqrt{6}$��M��N�ֱ�ΪPB��PD���е㣮
��ͼ��������P-ABCD�У������DZ߳�Ϊ2$\sqrt{3}$�����Σ��ҡ�BAD=120�㣬��PA��ƽ��ABCD��PA=2$\sqrt{6}$��M��N�ֱ�ΪPB��PD���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com