
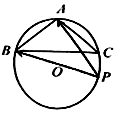
 ��ͼ���ڡ�A BC�У����ڽ� A��B��C�ĶԱ߷ֱ�Ϊa��b��c����a2=b2+c2+bc��$a=\sqrt{3}$��SΪ��A BC�������Բ O�ǡ�A BC�����Բ��P��Բ O��һ���㣬
��ͼ���ڡ�A BC�У����ڽ� A��B��C�ĶԱ߷ֱ�Ϊa��b��c����a2=b2+c2+bc��$a=\sqrt{3}$��SΪ��A BC�������Բ O�ǡ�A BC�����Բ��P��Բ O��һ���㣬���� ��1���������Ҷ����ͺ����Ҷ����Լ����Dz�����ҹ�ʽ�����Ǻ��������ʼ��������
��2������һ�������������������Լ����Ǻ��������ʼ��������
����������������ϵ�������������������㼴�����
��� �⣺��1����a2=b2+c2+bc��
��cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=-$\frac{1}{2}$��
��0�㣼A��180�㣬
��A=120��
�����Ҷ�����$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$⇒b=2sinB��c=2sinC
��$S+\sqrt{3}cos{B}cosC$=$\frac{1}{2}bcsinA+$$\sqrt{3}cos{B}cosC$=$\sqrt{3}sinBsinC+\sqrt{3}cos{B}cosC$=$\sqrt{6}$cos��B-C����$\sqrt{6}$��
���ҽ���B=Cʱȡ�Ⱥţ�
��$S+\sqrt{3}cos{B}cosC$���ֵΪ$\sqrt{6}$��
��2������һ����B=30��ʱ����A BCΪ���������Σ�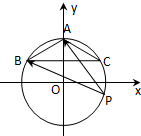
$\overrightarrow{{P}{A}}•\overrightarrow{{P}{B}}$�T$��\overrightarrow{PO}+\overrightarrow{OA}��•��\overrightarrow{PO}+\overrightarrow{OB}��={\overrightarrow{PO}^2}+\overrightarrow{PO}•��\overrightarrow{OA}+\overrightarrow{OB}��+\overrightarrow{OA}•\overrightarrow{OB}$=1+2$\overrightarrow{PO}•\overrightarrow{OD}$+$\frac{1}{2}$������DΪAB���е㣩
=$\frac{3}{2}+2|{\overrightarrow{PO}}||{\overrightarrow{OD}}|cos��\overrightarrow{PO}��\overrightarrow{OD}��$��$\frac{3}{2}+2��1��\frac{{\sqrt{3}}}{2}��1=\frac{3}{2}+\sqrt{3}$
��������OΪԭ�㣬OAΪ���ᣬ����ƽ��ֱ������ϵ����$A��0��1����B��-\frac{{\sqrt{3}}}{2}��\frac{1}{2}��$��
��P��cos�ȣ�sin�ȣ�����$\overrightarrow{PA}$=��-cos�ȣ�1-sin�ȣ���$\overrightarrow{PB}$=��-$\frac{\sqrt{3}}{2}$-cos�ȣ�$\frac{1}{2}$-sin�ȣ���
��$\overrightarrow{PA}$•$\overrightarrow{PB}$=cos2��+$\frac{\sqrt{3}}{2}$cos��+sin2��-$\frac{3}{2}$sin��+$\frac{1}{2}$=$\sqrt{3}$��$\frac{1}{2}$cos��-$\frac{\sqrt{3}}{2}$sin�ȣ�+$\frac{3}{2}$=$\sqrt{3}$cos����+$\frac{��}{3}$��+$\frac{3}{2}$��$\sqrt{3}$+$\frac{3}{2}$
���ҽ�����=$\frac{��}{6}$ʱȡ�Ⱥţ�
��$\overrightarrow{{P}{A}}•\overrightarrow{{P}{B}}$�����ֵΪ$\sqrt{3}$+$\frac{3}{2}$��
���� ���⿼���֪ʶ�������Ҷ��������Ҷ��������������������㣬�����Ǻ�����ƽ���������ۺ�Ӧ�ã��Ѷ��е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2\sqrt{3}}{5}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{4}{5}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
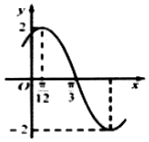 ��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ������f��x��ͼ�������е�����ƽ��$\frac{��}{12}$����λ�õ�����g��x����ͼ������g��x���ĵ����ݼ�����Ϊ��������
��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ������f��x��ͼ�������е�����ƽ��$\frac{��}{12}$����λ�õ�����g��x����ͼ������g��x���ĵ����ݼ�����Ϊ��������| A�� | [k��-$\frac{��}{3}$��k��+$\frac{��}{6}$]��k��Z | B�� | [k��+$\frac{��}{6}$��k��+$\frac{2��}{3}$]��k��Z | ||
| C�� | [k��-$\frac{��}{12}$��k��+$\frac{��}{12}$]��k��Z | D�� | [k��-$\frac{7��}{12}$��k��-$\frac{��}{12}$]��k��Z |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��0��x��4} | B�� | {x|x��-1��x��4} | C�� | R | D�� | {x|-1��x��0} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 6 | C�� | 5 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com