
分析 (1)根据椭圆的定义和性质,建立方程求出a,b即可.
(2)联立直线和椭圆方程,利用消元法结合设而不求的思想进行求解即可.
解答 解:(Ⅰ)∵点Q 在线段AP 的垂直平分线上,∴|AQ|=|PQ|.
又|CP|=|CQ|+|QP|=2$\sqrt{2}$,∴|CQ|+|QA|=2$\sqrt{2}$>|CA|=2.
∴曲线E是以坐标原点为中心,C(-1,0)和A(1,0)为焦点,长轴长为2$\sqrt{2}$ 的椭圆.
设曲线E 的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).
∵c=1,a=$\sqrt{2}$,∴b2=2-1=1.
∴曲线 E的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(Ⅱ)设M(x1,y1),N(x2,y2).
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$ 消去y,得(1+2k2)x2+4kmx+2m2-2=0.
此时有△=16k2-8m2+8>0.
由一元二次方程根与系数的关系,得x1+x2=$\frac{-4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-2}{1+2{k}^{2}}$,.
∴|MN|=$\sqrt{1+{k}^{2}}•\sqrt{(\frac{-4km}{1+2{k}^{2}})^{2}-4×\frac{2{m}^{2}-2}{1+2{k}^{2}}}$=$\frac{\sqrt{1+{k}^{2}}}{1+2{k}^{2}}$$•\sqrt{8(2{k}^{2}-{m}^{2}+1)}$
∵原点O到直线l的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$-,
∴S△MON=$\frac{1}{2}|MN|•d$=$\frac{\sqrt{2}}{1+2{k}^{2}}$.$\sqrt{{m}^{2}(2{k}^{2}-{m}^{2}+1)}$,由△>0,得2k2-m2+1>0.
又m≠0,
∴据基本不等式,得S△MON=$\frac{\sqrt{2}}{1+2{k}^{2}}$.$\sqrt{{m}^{2}(2{k}^{2}-{m}^{2}+1)}$≤$\frac{\sqrt{2}}{1+2{k}^{2}}$$•\frac{{m}^{2}+2{k}^{2}-{m}^{2}+1}{2}$=$\frac{\sqrt{2}}{2}$,
当且仅当m2=$\frac{2{k}^{2}+1}{2}$时,不等式取等号.
∴△MON面积的最大值为$\frac{\sqrt{2}}{2}$.
点评 本题主要考查与椭圆有关的轨迹方程问题,以及直线和椭圆的位置关系的应用,利用消元法以及设而不求的数学思想是解决本题的关键.,运算量较大,有一定的难度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
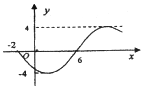
| A. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | B. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | C. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | 2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 3 | C. | -3 | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
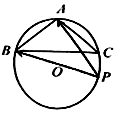 如图,在△A BC中,三内角 A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S为△A BC的面积,圆 O是△A BC的外接圆,P是圆 O上一动点,
如图,在△A BC中,三内角 A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S为△A BC的面积,圆 O是△A BC的外接圆,P是圆 O上一动点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com