
分析 设事件A表示“摸出第一只球为白球”,事件B表示“摸出第二只球为黄球”,则P(A)=$\frac{1}{6}$,P(AB)=$\frac{1}{10}$,由此利用条件概率计算公式能求出摸出第一只球为白球的情况下,第二只球为黄球的概率.
解答 解:设事件A表示“摸出第一只球为白球”,事件B表示“摸出第二只球为黄球”,
∵袋中有形状、大小都相同的6只球,其中1只白球,2只红球,3只黄球,从中随机先后摸出2只球,
∴P(A)=$\frac{1}{6}$,P(AB)=$\frac{1}{10}$,
∴摸出第一只球为白球的情况下,第二只球为黄球的概率:
P(B|A)=$\frac{P(AB)}{P(B)}$=$\frac{\frac{1}{10}}{\frac{1}{6}}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查概率的求法,涉及到条件概率等知识点,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想,是基础题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{7π}{12}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
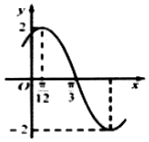 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)图象上所有点向右平移$\frac{π}{12}$个单位得到函数g(x)的图象,则函数g(x)的单调递减区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将f(x)图象上所有点向右平移$\frac{π}{12}$个单位得到函数g(x)的图象,则函数g(x)的单调递减区间为( )| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z | B. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z | ||
| C. | [kπ-$\frac{π}{12}$,kπ+$\frac{π}{12}$],k∈Z | D. | [kπ-$\frac{7π}{12}$,kπ-$\frac{π}{12}$],k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 观察下列各式:$\frac{3}{5}$<$\frac{3+1}{5+1}$,$\frac{3}{5}$<$\frac{3+2}{5+2}$,$\frac{3}{5}$<$\frac{3+3}{5+3}$,…,则$\frac{3}{5}$<$\frac{3+m}{5+m}$(m为正整数) | |
| B. | 观察(x2)′=2x,(x4)′=4x3,(cosx)′=-sinx,可得偶函数的导函数为奇函数 | |
| C. | 在平面上,若两个正三角形的边长比为1:2,则它们的面积比为1:4,类似的,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为1:8 | |
| D. | 所有平行四边形对角线互相平分,矩形是平行四边形,所以矩形的对角线互相平分 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 6 | C. | 5 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{3}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{5}}{5}$) | B. | ($\frac{\sqrt{5}}{5}$,1) | C. | (-∞,-1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com