
分析 根据数列{an}为上凸数列,且a1=1,a10=28,求出a3≥7…①.根据正整数n(1≤n<10,n∈N*),都有|an-bn|≤20,求出19≤a3≤19…②.问题得以解决
解答 解:∵$\frac{{{a_n}+{a_{n+2}}}}{2}≤{a_{n+1}}$,
∴an+an+2≤2an+1,
∴an+an+2≤2an+1,
∴an+2-an+1≤an+1-an,
∴$\frac{{a}_{n+2}-{a}_{n+1}}{(n+2)-(n+1)}$≤$\frac{{a}_{n+1}-{a}_{n}}{(n+1)-n}$,
∴$\frac{{a}_{10}-{a}_{1}}{10-1}$≤$\frac{{a}_{3}-{a}_{1}}{3-1}$
把a1=1,a10=28代入,得a3≥7…①.
在|an-bn|≤20,bn=n2-6n+10中,令n=3,得b3=9-18+10=1,
∴-20≤a3-b3≤20,
∴-19≤a3≤19…②.
①②联立得7≤a3≤19.
故答案为:[7,19].
点评 本题新定义的学习和应用,考查了学生的转化能力和运算能力,属于中档题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 是奇函数,且在(-∞,+∞)上是减函数 | B. | 是偶函数,且在(-∞,+∞)上是减函数 | ||
| C. | 是偶函数,且在(-∞,+∞)上是增函数 | D. | 是奇函数,且在(-∞,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
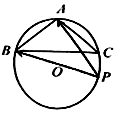 如图,在△A BC中,三内角 A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S为△A BC的面积,圆 O是△A BC的外接圆,P是圆 O上一动点,
如图,在△A BC中,三内角 A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S为△A BC的面积,圆 O是△A BC的外接圆,P是圆 O上一动点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 20 | C. | 16 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=sin2|x| | C. | y=-cos2x | D. | y=cos2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com