
分析 根据双曲线的定义得到|BF2|=a,|BF2|=3a,从而得到三角形F1AB是直角三角形,根据勾股定理建立方程关系即可得到结论.
解答 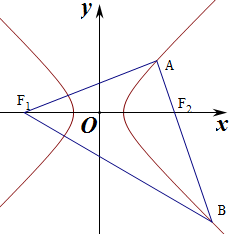 解:∵|AF1|=3a,|BF1|=5a,
解:∵|AF1|=3a,|BF1|=5a,
∴|AF1|-|BF2|=2a,|BF1|-|BF2|=2a,
则3a-|BF2|=2a,5a-|BF2|=2a,
即|BF2|=a,|BF2|=3a,
即|AB|=|BF2|+|BF2|=a+3a=4a,
则满足|AF1|2+|AB|2=|BF1|2,
则∠F1AB=90°,
则|AF1|2+|AF2|2=|F1F2|2,
即9a2+a2=4c2,
即10a2=4(a2+b2),
得3a2=2b2,
即$\frac{{b}^{2}}{{a}^{2}}$=$\frac{3}{2}$,即$\frac{b}{a}$=$\sqrt{\frac{3}{2}}$=$\frac{\sqrt{6}}{2}$,
即双曲线的渐近线方程为y=$±\frac{{\sqrt{6}}}{2}$x,
故答案为:y=$±\frac{{\sqrt{6}}}{2}$x.
点评 本题主要考查双曲线渐近线的求解,根据条件结合双曲线的定义判断三角形F1AB是直角三角形是解决本题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | -80 | -24 | 0 | 4 | 0 | 0 | 16 | 60 | 144 | 280 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=($\frac{1}{2}$)x | B. | f(x)=x2-4x+4 | C. | f(x)=|x+2| | D. | f(x)=log${\;}_{\frac{1}{2}}}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $sin\frac{20π}{3}<{0.3^π}<{π^{0.3}}$ | B. | $sin\frac{20π}{3}<{π^{0.3}}<{0.3^π}$ | ||
| C. | ${0.3^π}<sin\frac{20π}{3}<{π^{0.3}}$ | D. | ${0.3^π}<{π^{0.3}}<sin\frac{20π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1] | B. | (-1,1) | C. | ∅ | D. | [-1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com