
已知圆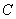 的半径为
的半径为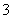 ,圆心
,圆心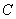 在直线
在直线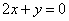 上,且在
上,且在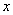 轴的下方,
轴的下方,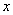 轴被圆
轴被圆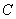 截得的弦长为
截得的弦长为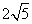 .
.
(Ⅰ)求圆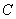 的方程;
的方程;
(Ⅱ)是否存在斜率为1的直线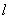 ,使
,使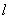 被圆
被圆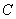 截得的弦
截得的弦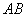 ,以
,以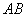 为直径的圆过原点?若存在求出直线
为直径的圆过原点?若存在求出直线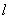 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
解: (Ⅰ)设圆心为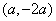
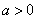
由勾股定理可得 (其中d是弦心距,MN是截得的弦长),
(其中d是弦心距,MN是截得的弦长),
即: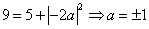 .又a > 0,则a =1,圆心(1,-2).
.又a > 0,则a =1,圆心(1,-2).
圆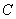 的标准方程是:
的标准方程是: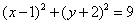 .
.
(Ⅱ)方法一:利用圆中的勾股定理(半径,半弦长,弦心距)解决问题.
设以AB为直径的圆M的圆心为M(a,b), 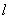 的斜率为1.在圆C中有
的斜率为1.在圆C中有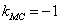 .
.
由C(1,-2)得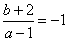 即b=-a-1.(*)
即b=-a-1.(*)
以AB为直径的圆过原点.OM=AM=BM=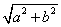
由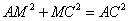 得
得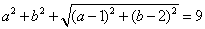
把(*)式代入上式,得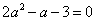 从而
从而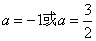 ,
,
故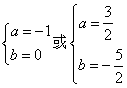
又(a,b)在直线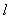 :x-y+m=0上,故m=b-a
:x-y+m=0上,故m=b-a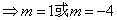 ,
,
∴直线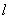 的方程为
的方程为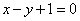 或
或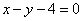 .
.
方法二:利用韦达定理解决问题
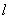 的斜率为1,可设
的斜率为1,可设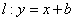 ,交点A
,交点A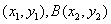 ,
,
圆C:  故
故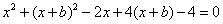
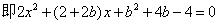 ①
①
韦达定理可得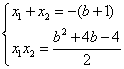 (◣)
(◣)
以AB为直径的圆过原点.则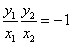 ,即 :
,即 :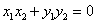 ,
,
故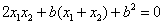 , 把(◣)式代入得
, 把(◣)式代入得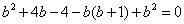
 ,∴
,∴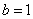 或
或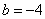
经检验: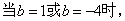 均能使①式中的判别式大于0成立,
均能使①式中的判别式大于0成立,
所以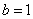 或
或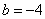 都是方程的解.
都是方程的解.
∴直线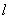 的方程为
的方程为 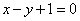 或
或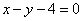 .
.


科目:高中数学 来源: 题型:
给出下列结论
①扇形的圆心角为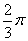 弧度,半径为2,则扇形的面积是
弧度,半径为2,则扇形的面积是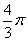 ;
;
②某小礼堂有25排座位,每排20个,一次心理学讲座,礼堂中坐满了学生,会后为了了解有关情况,留下座位号是15的所有25名学生进行测试,这里运用的是系统抽样方法;
③一个人打靶时连续射击两次,则事件“至少有一次中靶”与事件“两次都不中靶”互为对立事件;
④若数据: 的方差为8,则数据
的方差为8,则数据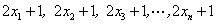 的方差为16;
的方差为16;
⑤相关系数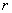 越大,表示两个变量相关性越强.
越大,表示两个变量相关性越强.
其中正确结论的序号为 . (把你认为正确结论的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com