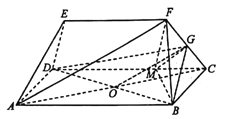
【题目】如图，在五面体
中，四边形
是矩形，
，
，
，
，
为
的中点，
为线段
上一点，且
.
（Ⅰ）求证：
平面
；
（Ⅱ）求证：
；
（Ⅲ）求证：平面
平面
.
【答案】(Ⅰ)证明见解析；(Ⅱ)证明见解析；(Ⅲ)证明见解析.
【解析】
试题分析：
(1)连接
交
于
点，则为的中点，连接
.由三角形中位线的性质可得
.结合线面平行的判定定理可得
平面
.
(2)连接
.由几何关系可证得四边形
是平行四边形.则
，结合直角三角形的性质和题意可得
，则
.
(3)由题意可知
为等边三角形，则
.同理可得
.利用线面垂直的判定定理可得
平面
，结合面面垂直的判定定理可得平面
平面
.
试题解析：
（Ⅰ）连接交于点，则为的中点，连接.
∵在
中，为的中点，
为
的中点.
∴.
∵
平面，
平面，
∴平面.
（Ⅱ）连接.
∵四边形
是矩形，
，
∴
，且
.
∵
，
，
，
∴
.
∵
，
，
∴
.
∴四边形是平行四边形.
∴，
.
∵在
中，
，
，，
∴
.
∵在
中，，
，
，
∴是直角三角形.
∴.
∴.
（Ⅲ）∵在中，
，
∴为等边三角形.
∵为的中点，
∴.
同理，由
为等边三角形，可得.
∵
，
∴平面.
∵
平面，
∴平面平面.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某快餐代卖店代售多种类型的快餐，深受广大消费者喜爱.其中，
种类型的快餐每份进价为
元，并以每份
元的价格销售.如果当天20:00之前卖不完，剩余的该种快餐每份以
元的价格作特价处理，且全部售完.
（1）若该代卖店每天定制
份种类型快餐，求种类型快餐当天的利润
（单位：元）关于当天需求量
（单位：份，
）的函数解析式；
（2）该代卖店记录了一个月
天的种类型快餐日需求量（每天20:00之前销售数量）
日需求量 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
（i）假设代卖店在这一个月内每天定制份种类型快餐，求这一个月种类型快餐的日利润（单位：元）的平均数（精确到
）；
（ii）若代卖店每天定制份种类型快餐，以天记录的日需求量的频率作为日需求量发生的概率，求种类型快餐当天的利润不少于
元的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
： 
经过椭圆
： 
的左右焦点
，且与椭圆
在第一象限的交点为
，且
三点共线，直线
交椭圆
于
， 
两点，且
（
）.
（1）求椭圆
的方程；
（2）当三角形
的面积取得最大值时，求直线
的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在R上的函数f（x）＞0，对任意x，y∈R都有f（x+y）＝f（x） f（y）成立，且当x＞0时，f（x）＞1．
（1）求f（0）的值；
（2）求证f（x）在R上是增函数；
（3）若f（k3x）f（3x﹣9x﹣2）＜1对任意x∈R恒成立，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，且当
时，
的最小值为2，
（1）求
的值，并求的单调递增区间.
（2）若将函数
的图象上的点的纵坐标不变，横坐标缩小到原来的
，再将所得的图象向右平移
个单位长度，得到函数
的图象，求方程
在区间
上所有根之和.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将
个编号为
、
、
、的不同小球全部放入个编号为、、、的个不同盒子中.求：
（1）每个盒至少一个球，有多少种不同的放法？
（2）恰好有一个空盒，有多少种不同的放法？
（3）每盒放一个球，并且恰好有一个球的编号与盒子的编号相同，有多少种不同的放法？
（4）把已知中个不同的小球换成四个完全相同的小球（无编号），其余条件不变，恰有一个空盒，有多少种不同的放法？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C： 
(a>b>0)的一个顶点为A(2,0)，离心率为
.直线y＝k(x－1)与椭圆C交于不同的两点M，N.
(1)求椭圆C的方程；
(2)当△AMN的面积为
时，求k的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，曲线
过点
，其参数方程为
（
为参数，
），以
为极点，
轴非负半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（1）求曲线的普通方程和曲线的直角坐标方程；
（2）求已知曲线和曲线交于
，
两点，且
，求实数
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
