解:(1)由题意令y=f(x)=x
a,由于图象过点(

,

),
得

=
 a
a,a=-1
∴y=f(x)=x
-1(2)g(x)=f(x)+x=x+

函数

在区间(1,+∞)上是增函数,
证明:任取x
1、x
2使得x
1>x
2>1,
都有

由x
1>x
2>1得,x
1-x
2>0,x
1x
2>0,x
1x
2-1>0,
于是g(x
1)-g(x
2)>0,即g(x
1)>g(x
2),
所以,函数

在区间(1,+∞)上是增函数.
分析:(1)先由幂函数的定义用待定系数法设出其解析式,代入点的坐标,求出幂函数的解析式即可;
(2)函数在区间(1,+∞)上为增函数,理由为:在区间(1,+∞)上任取x
1>x
2>1,求出f(x
1)-f(x
2),通分后,根据设出的x
1>x
2>1,判定其差大于0,即f(x
1)>f(x
2),从而得到函数为增函数.
点评:本题考查幂函数的单调性、奇偶性及其应用,解题的关键是熟练掌握幂函数的性质,能根据幂函数的性质求其解析式,求函数值.

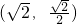 .
. ,
, ),
), =
= a,a=-1
a,a=-1
 在区间(1,+∞)上是增函数,
在区间(1,+∞)上是增函数,
 在区间(1,+∞)上是增函数.
在区间(1,+∞)上是增函数.
