
平面内有12个点,其中有4个点共线,此外再无任何3点共线,以这些点为顶点,可得多少个不同的三角形?
科目:高中数学 来源: 题型:解答题
(14分)已知在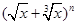 (其中n<15)的展开式中:
(其中n<15)的展开式中:
(1)求二项式展开式中各项系数之和;
(2)若展开式中第9项,第10项,第11项的二项式系数成等差数列,求n的值;
(3)在(2)的条件下写出它展开式中的有理项.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在以AB为直径的半圆周上,有异于A,B的六个点C1,C2,…,C6,直径AB上有异于A,B的四个点D1,D2,D3,D4.则:
(1)以这12个点(包括A,B)中的4个点为顶点,可作出多少个四边形?
(2)以这10个点(不包括A,B)中的3个点为顶点,可作出多少个三角形?其中含点C1的有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知10件不同产品中共有4件次品,现对它们进行一一测试,直至找到所有次品为止.
(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品的不同测试方法数有多少种?
(2)若恰在第5次测试后,就找出了所有次品,则这样的不同测试方法数有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
三个女生和五个男生排成一排.
(1)如果女生必须全排在一起,有多少种不同的排法?
(2)如果女生必须全分开,有多少种不同的排法?
(3)如果两端都不能排女生,有多少种不同的排法?
(4)如果两端不能都排女生,有多少种不同的排法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com