
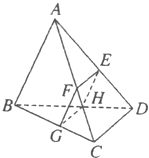
 如图所示,已知三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,求证:
如图所示,已知三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,求证:

科目:高中数学 来源: 题型:
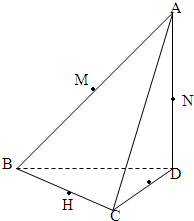 如图所示,已知三棱锥A-BCD中,AD⊥平面BCD点M、N、G、H分别是棱AB、AD、DC、CB的中点.
如图所示,已知三棱锥A-BCD中,AD⊥平面BCD点M、N、G、H分别是棱AB、AD、DC、CB的中点.| 2 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
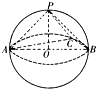 如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC,
如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC,| AB |
| BC |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
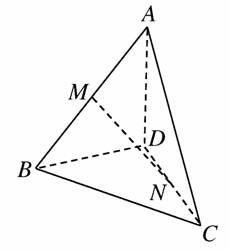
如图所示,已知三棱锥A-BCD中M、N分别为AB、CD的中点,则下列结论正确的是( )
A.MN≥![]() (AC+BD)
(AC+BD)
B.MN≤![]() (AC+BD)
(AC+BD)
C.MN=![]() (AC+BD)
(AC+BD)
D.MN<![]() (AC+BD)
(AC+BD)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年宁夏高三上学期第五次月考文科数学试卷(解析版) 题型:解答题
如图所示,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
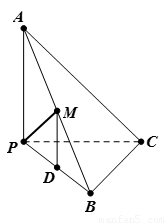
(1)求证:DM∥平面APC; (2)求证:平面ABC⊥平面APC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com