
如图所示,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
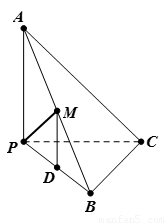
(1)求证:DM∥平面APC; (2)求证:平面ABC⊥平面APC.
(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)要证明直线和平面平行,只需在平面内找一条 直线与之平行,由已知得 是
是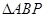 的中位线,所以
的中位线,所以 ,进而证明
,进而证明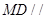 平面
平面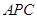 ;(2)要证明面面垂直,只需在一个平面内找到另一个平面的一条垂线即可,由等边三角形
;(2)要证明面面垂直,只需在一个平面内找到另一个平面的一条垂线即可,由等边三角形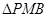 及
及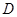 为
为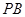 的中点,则
的中点,则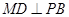 ,进而说明
,进而说明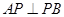 ,进而说明
,进而说明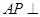 平面
平面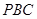 ,则有
,则有 ,又由已知
,又由已知 可证
可证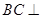 平面
平面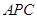 ,进而证明结论.
,进而证明结论.
试题解析:(1)由已知,得 是
是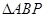 的中位线,所以
的中位线,所以 ,又
,又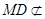 平面
平面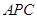 ,
,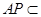 平面
平面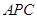 ,故
,故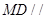 平面
平面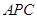 .
.
(2)因为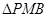 为正三角形,
为正三角形,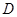 为
为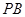 的中点,所以
的中点,所以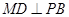 .所以
.所以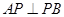 .又
.又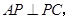
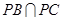
所以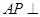 平面
平面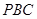 .因为
.因为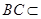 平面
平面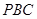 ,所以
,所以 .又
.又
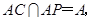 所以
所以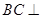 平面
平面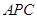 .因为
.因为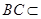 平面
平面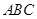 ,所以平面
,所以平面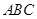 ⊥平面
⊥平面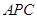 .
.
考点:1、直线和平面平行的判定;2、直线和平面垂直的判定和性质;3、面面垂直的判定.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
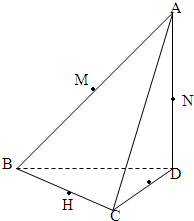 如图所示,已知三棱锥A-BCD中,AD⊥平面BCD点M、N、G、H分别是棱AB、AD、DC、CB的中点.
如图所示,已知三棱锥A-BCD中,AD⊥平面BCD点M、N、G、H分别是棱AB、AD、DC、CB的中点.| 2 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
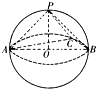 如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC,
如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC,| AB |
| BC |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
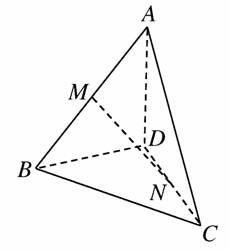
如图所示,已知三棱锥A-BCD中M、N分别为AB、CD的中点,则下列结论正确的是( )
A.MN≥![]() (AC+BD)
(AC+BD)
B.MN≤![]() (AC+BD)
(AC+BD)
C.MN=![]() (AC+BD)
(AC+BD)
D.MN<![]() (AC+BD)
(AC+BD)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com