
某地区为了解高二学生作业量和玩电脑游戏的情况,对该地区内所有高二学生采用随机抽样的方法,得到一个容量为200的样本.统计数据如下:
(1)已知该地区共有高二学生42500名,根据该样本估计总体,其中喜欢电脑游戏并认为作业不多的人有多少名?
(2)在A,B,C,D,E,F六名学生中,仅有A,B两名学生认为作业多.如果从这六名学生中随机抽取两名,求至少有一名学生认为作业多的概率.
(1)7650名;(2)
解析试题分析:(1)利用样本估计总体,可求得喜欢电脑游戏并认为作业不多的人数;(2)用列举法,并利用古典概型即可求得至少有一名学生认为作业多的概率
试题解析:(1)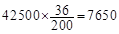 (名) 5分
(名) 5分
(2)【方法一】从这六名学生中随机抽取两名的基本事件有:{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}共15个 7分
其中至少有一个学生认为作业多的事件有{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F}共9个 9分
∴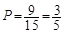
即至少有一名学生认为作业多的概率为 . 12分
. 12分
【方法二】6名学生中随机抽取2名的选法有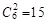 种, 7分
种, 7分
其中至少有一名学生认为作业多的选法有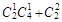 =9种, 9分
=9种, 9分
∴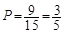
即至少有一名学生认为作业多的概率为 . 12分
. 12分
【方法三】6名学生中随机抽取2名的选法有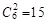 种, 7分
种, 7分
其中没有人认为作业多的选法有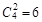 种 9分
种 9分
∴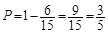
即至少有一名学生认为作业多的概率为 . 12分
. 12分
考点:统计,随机抽样,用样本估计总体,古典概型.


科目:高中数学 来源: 题型:解答题
在平面 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为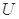 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
.
(1)定义横、纵坐标为整数的点为“整点”.在区域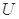 任取3个整点,求这些整点中恰有2个整点在区域
任取3个整点,求这些整点中恰有2个整点在区域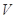 的概率;
的概率;
(2)在区域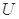 每次任取
每次任取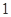 个点,连续取
个点,连续取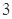 次,得到
次,得到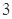 个点,记这
个点,记这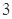 个点在区域
个点在区域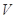 的个数为
的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知方程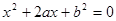 是关于
是关于 的一元二次方程.
的一元二次方程.
(1)若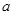 是从集合
是从集合 四个数中任取的一个数,
四个数中任取的一个数,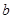 是从集合
是从集合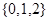 三个数中任取的一个数,求上述方程有实数根的概率;
三个数中任取的一个数,求上述方程有实数根的概率;
(2)若 ,
, ,求上述方程有实数根的概率.
,求上述方程有实数根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
甲、乙两人各进行3次射击,甲每次击中目标的概率为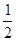 ,乙每次击中目标的概率
,乙每次击中目标的概率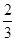 .
.
(1)记甲击中目标的次数为ξ,求ξ的概率分布列及数学期望Eξ;
(2)求甲恰好比乙多击中目标2次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩,乙组记录中有一个数字模糊,无法确认.假设这个数字具有随机性,并在图中以a表示.
(1)若甲、乙两个小组的数学平均成绩相同,求a的值;
(2)求乙组平均成绩超过甲组平均成绩的概率;
(3)当a=2时,分别从甲、乙两组中各随机选取一名同学,设这两名同学成绩之差的绝对值为X,求随机变量X的分布列和数学期望,
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产A,B两种元件,其质量按测试指标划分,指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100个进行检测,检测结果统计如下:
| 测试 指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校夏令营有3名男同学 和3名女同学
和3名女同学 ,其年级情况如下表:
,其年级情况如下表:
| | 一年级 | 二年级 | 三年级 |
| 男同学 | A | B | C |
| 女同学 | X | Y | Z |
 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件 发生的概率.
发生的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com