已知函数f(x)=x2+ax+b
(1)若对任意的实数x都有f (1+x)=f (1-x) 成立,求实数 a的值;
(2)若f(x)为偶函数,求实数a的值;
(3)若f(x)在[1,+∞)内递增,求实数a的范围.
解:(1)∵f(1+x)=f(1-x)
∴y=f(x)的图象关于直线x=1对称
∴
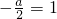
即a=-2
(2)∵f(x)为偶函数,
∴f(-x)=f(x)对于一切实数x恒成立
即(-x)
2+a(-x)+b=x
2+ax+b
∴2ax=0
∴a=0
(3)∵f(x)在[1,+∞)内递增
∴
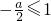
∴a≥-2
即实数a的范围为[-2,+∞)
分析:(1)由已知中对任意的实数x都有f (1+x)=f (1-x) 成立,结合函数的对称性,我们易得到函数的图象的对称轴为直线x=1,结合二次函数的性质我们可以构造一个关于a的方程,解方程即可求出实数 a的值;
(2)根据偶函数的定义,我们可得f(-x)=f(x)恒成立,代入即可构造一个关于实数a的方程,解方程即可求出实数 a的值;
(3)f(x)在[1,+∞)内递增,则表示区间[1,+∞)在函数对称轴的右侧,由此可以构造一个关于a的不等式,解不等式即可求出实数 a的范围.
点评:本题考查的知识点是二次函数的性质,其中根据二次函数的图象和性质构造出关于a的方程(或不等式是解答本题的关键).

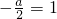 即a=-2
即a=-2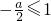


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<