
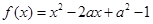 .
.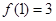 ,求实数
,求实数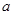 的值;
的值;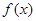 在区间
在区间 上是单调的,求实数
上是单调的,求实数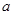 的取值范围;
的取值范围;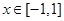 时,求函数
时,求函数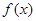 的最小值
的最小值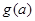 .
.科目:高中数学 来源:不详 题型:解答题
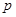 元(即税率为
元(即税率为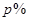 ),因此每年销量将减少
),因此每年销量将减少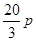 万件.
万件.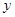 (万元),表示成
(万元),表示成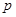 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;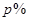 应怎样确定?
应怎样确定?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
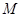 是满足下列性质函数的
是满足下列性质函数的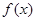 的全体,在定义域
的全体,在定义域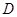 内存在
内存在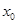 ,使得
,使得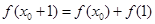 成立。(1)函数
成立。(1)函数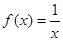 ,
,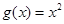 是否属于集合
是否属于集合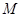 ?分别说明理由。(2)若函数
?分别说明理由。(2)若函数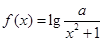 属于集合
属于集合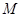 ,求实数
,求实数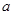 的取值范围。
的取值范围。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com