
【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
【答案】(Ⅰ)见解析;(Ⅱ)作图见解析,体积为![]() .
.
【解析】试题分析:证明![]() 由
由![]() 可得
可得![]() 是
是![]() 的中点.(Ⅱ)在平面
的中点.(Ⅱ)在平面![]() 内,过点
内,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,
, ![]() 即为
即为![]() 在平面
在平面![]() 内的正投影.根据正三棱锥的侧面是直角三角形且
内的正投影.根据正三棱锥的侧面是直角三角形且![]() ,可得
,可得![]() 在等腰直角三角形
在等腰直角三角形![]() 中,可得
中,可得![]() 四面体
四面体![]() 的体积
的体积![]()
试题解析:(Ⅰ)因为![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,所以
,所以![]()
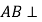
因为![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,所以
,所以![]()
所以![]() 平面
平面![]() ,故
,故![]()
又由已知可得, ![]() ,从而
,从而![]() 是
是![]() 的中点.
的中点.
(Ⅱ)在平面![]() 内,过点
内,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,
, ![]() 即为
即为![]() 在平面
在平面![]() 内的正投影.
内的正投影.
理由如下:由已知可得![]()
![]() ,
, ![]() ,又
,又![]() ,所以
,所以![]() ,因此
,因此![]() 平面
平面![]() ,即点
,即点![]() 为
为![]() 在平面
在平面![]() 内的正投影.
内的正投影.
连结![]() ,因为
,因为![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,所以
,所以![]() 是正三角形
是正三角形![]() 的中心.
的中心.
由(Ⅰ)知, ![]() 是
是![]() 的中点,所以
的中点,所以![]() 在
在![]() 上,故
上,故![]()
由题设可得![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,因此
,因此![]()
由已知,正三棱锥的侧面是直角三角形且![]() ,可得
,可得![]()
在等腰直角三角形![]() 中,可得
中,可得![]()
所以四面体![]() 的体积
的体积![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了保证食品的安全卫生,食品监督管理部门对某食品厂生产甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克).规定:当食品中的有害微量元素的含量在![]() 时为一等品,在
时为一等品,在![]() 为二等品,20以上为劣质品.
为二等品,20以上为劣质品.

(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个,求抽到食品甲包含劣质品的概率和抽到食品乙全是一等品的概率;
(2)在概率和统计学中,数学期望(或均值)是基本的统计概念,它反映随机变量取值的平均水平.变量的一切可能的取值![]() 与对应的概率
与对应的概率![]() 乘积之和称为该变量的数学期望,记为
乘积之和称为该变量的数学期望,记为![]() .
.
参考公式:变量![]() 的取值为
的取值为![]() ,
,![]() 对应取值的概率
对应取值的概率![]() ,可理解为数据
,可理解为数据![]() 出现的频率
出现的频率![]() ,
,
![]()
![]() .
.
①每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元,根据上表统计得到甲、乙两种食品为一等品、二等品、劣质品的频率,分别估计这两种食品为一等品、 二等品、劣质品的概率,若分别从甲、乙食品中各抽取1件,求这两件食品各自能给该厂 带来的盈利期望![]() .
.
②若生产食品甲初期需要一次性投入10万元,生产食品乙初期需要一次性投人16 万元,但是以目前企业的状况,甲乙两条生产线只能投资其中一条.如果你是该食品厂负责人,以一年为期限,盈利为参照,请给出合理的投资方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),过原点的两条直线
为参数),过原点的两条直线![]() 分别与曲线
分别与曲线![]() 交于异于原点的
交于异于原点的![]() 、
、![]() 两点,且
两点,且![]() ,其中
,其中![]() 的倾斜角为
的倾斜角为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 和
和![]() 的极坐标方程;
的极坐标方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为
的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为![]() .
.
(1)求椭圆C的方程;
(2)若直线l:y=kx+m(k,m∈R)与椭圆C交于A,B两点,O为坐标原点,△AOB的重心G满足: ![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.

(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对顾客实行购物优惠活动规定,一次购物付款总额:
(1)如果标价总额不超过200元,则不给予优惠;
(2)如果标价总额超过200元但不超过500元,则按标价总额给予9折优惠;
(3)如果标价总额超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予8折优惠.
某人两次去购物,分别付款180元和423元,假设他一次性购买上述两次同样的商品,则应付款( )
A.550元B.560元C.570元D.580元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com