
分析 (1)判断3×9=27,10+9+8=27,得出甲得到27分的概率为($\frac{1}{4}$)3+${C}_{3}^{1}$×$\frac{1}{4}$${×C}_{2}^{1}$×$\frac{1}{4}$×$\frac{1}{2}$,
(2)利用给出的数据得出:甲得到的分数是ξ=24,25,26,27,28,29,30,求解概率得出分布列,数学期望.
解答 解:∵设x1=10,x2=9,x3=8,
∴P(x1)=$\frac{1}{4}$,P(x2)=$\frac{1}{4}$,P(x3)=$\frac{1}{2}$,
(1)∵3×9=27,10+9+8=27
∴甲得到27分的概率为($\frac{1}{4}$)3+${C}_{3}^{1}$×$\frac{1}{4}$${×C}_{2}^{1}$×$\frac{1}{4}$×$\frac{1}{2}$=$\frac{13}{64}$,
(2)∵甲得到的分数是ξ=24,25,26,27,28,29,30,
∴P(ξ=24)=${C}_{3}^{3}$×($\frac{1}{2}$)3=$\frac{1}{8}$,
P(ξ=25)=${C}_{3}^{2}$($\frac{1}{2}$)2×$\frac{1}{4}$=$\frac{3}{16}$,
P(ξ=26)=${C}_{3}^{2}$($\frac{1}{4}$)2×$\frac{1}{2}$+${C}_{3}^{2}$($\frac{1}{2}$)2×$\frac{1}{4}$=$\frac{9}{32}$,
P(27)=$\frac{13}{64}$
P(ξ=28)=${C}_{3}^{2}$×($\frac{1}{4}$)2×$\frac{1}{2}$+${C}_{3}^{2}$×($\frac{1}{4}$)2×$\frac{1}{4}$=$\frac{9}{64}$,
P(ξ=29))=${C}_{3}^{2}$×($\frac{1}{4}$)2×$\frac{1}{4}$=$\frac{3}{64}$,
P(ξ=30)=${C}_{3}^{3}$×($\frac{1}{4}$)3=$\frac{1}{64}$,
| ξ | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| P | $\frac{1}{8}$ | $\frac{3}{16}$ | $\frac{9}{32}$ | $\frac{13}{64}$ | $\frac{9}{64}$ | $\frac{3}{64}$ | $\frac{1}{64}$ |
点评 本题考查了离散型的概率问题在实际问题中的应用,关键是确定随机变量的数据及构成因素,得出概率分布,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|$\frac{1}{2}$<x≤1} | C. | {x|x<1} | D. | {x|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
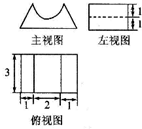
| A. | 27-$\frac{3π}{2}$ | B. | 18-$\frac{3π}{2}$ | C. | 27-3π | D. | 18-3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
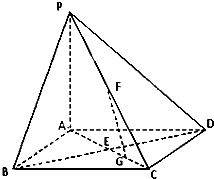 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com