Question

（06年江西卷理）（14分）

已知数列｛a_n｝满足：a₁＝，且a_n＝

（1）求数列｛a_n｝的通项公式；

（2）证明：对于一切正整数n，不等式a₁?a₂?……a_n<2?n！

Answer 1

解析：（1）将条件变为：1－＝，因此｛1－｝为一个等比数列，其首项为

1－＝，公比，从而1－＝，据此得a_n＝（n³1）…………1°

（2）证：据1°得，a₁?a₂?…a_n＝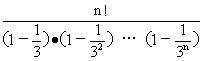

为证a₁?a₂?……a_n<2?n！

只要证nÎN^*时有>…………2°

显然，左端每个因式都是正数，先证明，对每个nÎN^*，有

³1－（）…………3°

用数学归纳法证明3°式：

（i）                     n＝1时，3°式显然成立，

（ii）                   设n＝k时，3°式成立，

即³1－（）

则当n＝k＋1时，

³〔1－（）〕?（）

＝1－（）－＋（）

³1－（＋）即当n＝k＋1时，3°式也成立。

故对一切nÎN^*，3°式都成立。

利用3°得，³1－（）＝1－

＝1－>

故2°式成立，从而结论成立。