
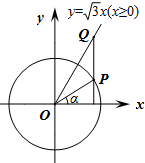
 如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).分析 (Ⅰ)首先根据函数的图象求出角的正弦值和余弦值,进一步求出结果.
(Ⅱ)利用三角函数的恒等变换,进一步求出函数的正弦形式,最后求出函数的最值.
解答  解:(Ⅰ)如图所示:∠MOQ=$\frac{π}{3}$,
解:(Ⅰ)如图所示:∠MOQ=$\frac{π}{3}$,
所以:$∠POQ=\frac{π}{3}-α$,
由于:sinα=$\frac{1}{3}$$\begin{array}{c},\end{array}\right.$$α∈(-\frac{π}{2},\frac{π}{2})$,
所以:$cosα=\frac{2\sqrt{2}}{3}$,
cos∠POQ=cos($\frac{π}{3}-α$)=$cos\frac{π}{3}cosα+sin\frac{π}{3}sinα$=$\frac{2\sqrt{2}+\sqrt{3}}{6}$.
(Ⅱ)由于P(cosα,sinα),
所以:Q(cosα,$\sqrt{3}$cosα),
则${S}_{△POQ}=\frac{1}{2}|cosα||\sqrt{3}cosα-sinα|$
=$\frac{1}{2}|\sqrt{3}{cos}^{2}α-sinαcosα|$
=$\frac{1}{2}|\frac{\sqrt{3}}{2}cos2α-\frac{sin2α}{2}|$
=$\frac{1}{2}|sin(\frac{π}{3}-α)+\frac{\sqrt{3}}{2}$|
$≤\frac{1}{2}|\frac{\sqrt{3}}{2}+1|=\frac{\sqrt{3}}{4}+\frac{1}{2}$,
所以:△POQ面积的最大值为:$\frac{\sqrt{3}}{4}+\frac{1}{2}$.
点评 本题考查的知识要点:三角函数关系式的恒等变换,三角函数的最值问题及相关的运算.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:解答题
有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上上分别写着数字1,2,3,5,同时投掷这两枚玩具一次,记 为两个朝下的面上的数字之和.
为两个朝下的面上的数字之和.
(1)求事件“ 不小于6”的概率;
不小于6”的概率;
(2)“ 为奇数”的概率和“
为奇数”的概率和“ 为偶数”的概率是不是相等?证明你作出的结论.
为偶数”的概率是不是相等?证明你作出的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com