
分析 (1)分子分母同除以cosα,由同角三角函数关系式即可得解.
(2)由倍角公式和万能公式化简后结合已知即可得解.
(3)由倍角公式和万能公式化简后结合已知即可得解.
解答 解:∵tanα=-$\frac{1}{3}$,
(1)$\frac{4sinα-2cosα}{5cosα+3sinα}$=$\frac{4tanα-2}{5+3tanα}$=$\frac{4×(-\frac{1}{3})-2}{5+3×(-\frac{1}{3})}$=-$\frac{5}{6}$;
(2)∵sin2α=$\frac{2tanα}{1+ta{n}^{2}α}$=-$\frac{3}{5}$,cos2α=$\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$=$\frac{4}{5}$
∴2sin2α-$\frac{3}{2}$sinαcosα+5cos2α=1-cos2α-$\frac{3}{4}$sin2α+$\frac{5}{2}$(1+cos2α)=$\frac{7}{2}$-$\frac{3}{4}$sin2α+$\frac{3}{2}$cos2α=$\frac{7}{2}$-$\frac{3}{4}$×(-$\frac{3}{5}$)+$\frac{3}{2}$×$\frac{4}{5}$=$\frac{103}{20}$;
(3)$\frac{1}{1-sinαcosα}$=$\frac{1}{1-\frac{1}{2}sin2α}$=$\frac{1}{1-\frac{1}{2}×\frac{2tanα}{1+ta{n}^{2}α}}$=$\frac{10}{13}$.
点评 本题主要考查了倍角公式,万能公式,同角三角函数关系式的应用,属于基本知识的考查.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ±2 | B. | ±$\sqrt{3}$ | C. | ±$\frac{2\sqrt{3}}{3}$ | D. | ±3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$+1 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
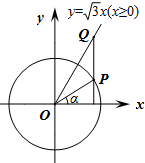 如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源:2017届云南曲靖市高三上半月考一数学试卷(解析版) 题型:选择题
在区间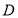 上,若函数
上,若函数 为增函数,而函数
为增函数,而函数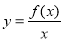 为减函数,则称函数
为减函数,则称函数 为区间
为区间 上的“弱增”函数.则下列函数中,在区间
上的“弱增”函数.则下列函数中,在区间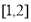 上不是“弱增”函数的为( )
上不是“弱增”函数的为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com