练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设椭圆的方程为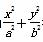＝1(a>b>0)，a∈{1,2,3,4,5,6,7}，b∈{1,2,3,4,5}，这样的椭圆共有多少个？


    解　依题意按a，b的取值分为6类，

    第一类：a＝2，b＝1；

    第二类：a＝3，b＝1,2；

    第三类：a＝4，b＝1,2,3；

    第四类：a＝5，b＝1,2,3,4；

    第五类：a＝6，b＝1,2,3,4,5；

    第六类：a＝7，b＝1,2,3,4,5.

    由分类计数原理得：这样的椭圆共有1＋2＋3＋4＋5＋5＝20(个)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    .第20届世界杯足球赛于2014年夏季在巴西举办，共32支球队有幸参加，它们先分成8个小组进行循环赛，决出16强(每队均与本组其他队赛一场，各组一、二名晋级16强)，这

      16支球队按确定的程序进行淘汰赛，最后决出冠、亚军，此外还要决出第三名、第四名，问这届世界杯总共将进行多少场比赛？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    三名教师教六个班的数学，则每人教两个班，分配方案共有________种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用0,1,2,3,4,5这六个数字，完成下面三个小题．

    (1)若数字允许重复，可以组成多少个不同的五位偶数；

    (2)若数字不允许重复，可以组成多少个能被5整除的且百位数字不是3的不同的五位数；

    (3)若直线方程ax＋by＝0中的a、b可以从已知的六个数字中任取2个不同的数字，则直线方程表示的不同直线共有多少条？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    植树节那天，四位同学植树，现有3棵不同的树，若一棵树限1人完成，则不同的植树方法种数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现有4种不同颜色对如图所示的四个部分进行着色，要求有公共边界的两块不能用同一种颜色，则不同的着色方法共有________种．                                             

       

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    从{－3，－2，－1,0,1,2,3}中，任取3个不同的数作为抛物线方程y＝ax2＋bx＋c的系数，如果抛物线经过原点，且顶点在第一象限，则这样的抛物线共有多少条？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若A＝17×16×15×…×5×4，则n＝______，m＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)是定义在R上的周期为2的函数，且是偶函数，已知当x∈[2,3]时，f(x)=x，则当x∈[－2，0]时f(x)的解析式是          .

    查看答案和解析>>

    同步练习册答案