
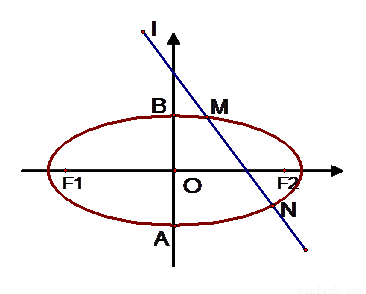
(12分)如图所示,椭圆C: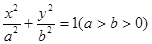 的离心率
的离心率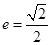 ,左焦点为
,左焦点为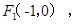 右焦点为
右焦点为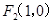 ,短轴两个端点为
,短轴两个端点为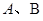 .与
.与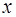 轴不垂直的直线
轴不垂直的直线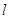 与椭圆C交于不同的两点
与椭圆C交于不同的两点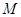 、
、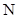 ,记直线
,记直线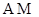 、
、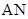 的斜率分别为
的斜率分别为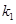 、
、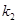 ,且
,且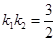 .
.
(1)求椭圆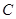 的方程;
的方程;
(2)求证直线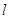 与
与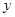 轴相交于定点,并求出定点坐标.
轴相交于定点,并求出定点坐标.
(3)当弦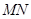 的中点
的中点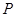 落在
落在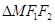 内(包括边界)时,求直线
内(包括边界)时,求直线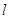 的斜率的取值。
的斜率的取值。
(1)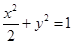 .(2)直线
.(2)直线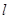 与
与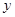 轴相交于定点(0,2);(3)
轴相交于定点(0,2);(3)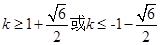 。
。
【解析】
试题分析:(1)由题意可知:椭圆C的离心率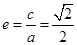 ,
,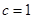
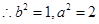
故椭圆C的方程为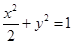 .…………………………………………………2分
.…………………………………………………2分
(2)设直线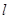 的方程为
的方程为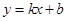 ,M、N坐标分别为
,M、N坐标分别为 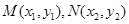
由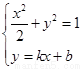 得
得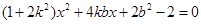
∴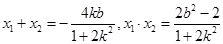 …………………………………………………4分
…………………………………………………4分
∵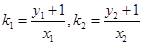 .
.
∴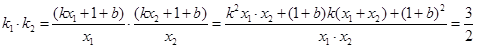
将韦达定理代入,并整理得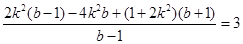 ,解得
,解得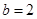 .
.
∴直线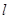 与
与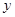 轴相交于定点(0,2)………………………………………………7分
轴相交于定点(0,2)………………………………………………7分
(3)由(2)中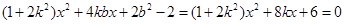 ,其判别式
,其判别式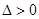 ,得
,得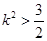 .①
.①
设弦AB的中点P坐标为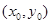 ,则
,则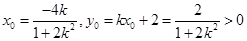 ,
,
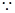 弦
弦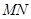 的中点
的中点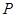 落在
落在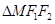 内(包括边界)
内(包括边界)
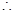
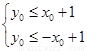
将坐标代入,整理得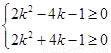
解得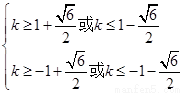 ②由①②得所求范围为
②由①②得所求范围为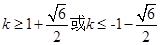 ……………………………………12分
……………………………………12分
考点:本题主要考查椭圆标准方程,椭圆的几何性质,直线与椭圆的位置关系,不等式组解法。
点评:求椭圆的标准方程是解析几何的基本问题,涉及直线与椭圆的位置关系问题,常常运用韦达定理,本题属于中档题。


 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
 如图所示,椭圆C:
如图所示,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| OB |
| F1B |
| |F1F2 |
| F1B |
| |F1F2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,椭圆C:
如图所示,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,椭圆C:
如图所示,椭圆C:| x2 |
| b2 |
| y2 |
| a2 |
| F2B |
| AF2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,椭圆C:
如图所示,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•茂名二模)如图所示,椭圆C:
(2010•茂名二模)如图所示,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com