
【题目】已知函数f(x)![]() ,
,
(1)讨论函数f(x)的单调性;
(2)证明:a=1时,f(x)+g(x)﹣(1![]() )lnx>e.
)lnx>e.
【答案】(1)详见解析;(2)证明见解析
【解析】
(1)对![]() 求导后,再对a分类讨论即可得出函数的单调性.
求导后,再对a分类讨论即可得出函数的单调性.
(2)a=1时,将所证不等式转化为ex﹣ex+1![]() ,令F(x)=ex﹣ex+1,G(x)
,令F(x)=ex﹣ex+1,G(x)![]() ,分别根据导数求出
,分别根据导数求出![]() 的最小值和
的最小值和![]() 的最大值即可证明不等式成立.
的最大值即可证明不等式成立.
(1)f(x)![]() alnx,(x∈(0,+∞)).
alnx,(x∈(0,+∞)).
![]()
![]() .
.
当a≤0时,![]() <0,函数f(x)在x∈(0,+∞)上单调递减.
<0,函数f(x)在x∈(0,+∞)上单调递减.
a>0时,由![]()
![]() ,得
,得![]() ,由
,由![]()
![]() ,得
,得![]()
所以函数![]() 在(0,
在(0,![]() )上单调递减,在(
)上单调递减,在(![]() ,+∞)上单调递增.
,+∞)上单调递增.
(2)证明:a=1时,要证f(x)+g(x)﹣(1![]() )lnx>e.
)lnx>e.
即要证:![]() lnx﹣e>0ex﹣ex+1
lnx﹣e>0ex﹣ex+1![]() .x∈(0,+∞).
.x∈(0,+∞).
令F(x)=ex﹣ex+1,F′(x)=ex﹣e,
当x∈(0,1)时,F′(x)<0,此时函数F(x/span>)单调递减;
当x∈(1,+∞)时,F′(x)>0,此时函数F(x)单调递增.
可得x=1时,函数F(x)取得最小值,F(1)=1.
令G(x)![]() ,G′(x)
,G′(x)![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() 为增函数,
为增函数,
当![]() 时。
时。![]() ,此时
,此时![]() 为减函数
为减函数
所以x=e时,函数G(x)取得最大值,G(e)=1.
x=1与x=e不同时取得,因此F(x)>G(x),即ex﹣ex+1![]() .x∈(0,+∞).
.x∈(0,+∞).
故原不等式成立.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos2x+ax2.
(1)当a=1时,求f(x)的导函数![]() 在
在![]() 上的零点个数;
上的零点个数;
(2)若关于x的不等式2cos(2sinx)+a2x2≤af(x)在(﹣∞,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线![]() 是过点
是过点![]() 的动直线,当
的动直线,当![]() 与圆
与圆![]() 相切时,同时也和抛物线
相切时,同时也和抛物线![]() 相切.
相切.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,与圆
,与圆![]() 交于不同的两点A、B,
交于不同的两点A、B,![]() 面积为
面积为![]() ,
,![]() 面积为
面积为![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 则x∈[﹣1,e]时,f(x)的最小值为_____;设g(x)=[f(x)]2﹣f(x)+a若函数g(x)有6个零点,则实数a的取值范围是_____.
则x∈[﹣1,e]时,f(x)的最小值为_____;设g(x)=[f(x)]2﹣f(x)+a若函数g(x)有6个零点,则实数a的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“未来肯定是非接触的,无感支付的方式将成为主流,这有助于降低交互门槛”.云从科技联合创始人姚志强告诉南方日报记者.相对于主流支付方式二维码支付,刷脸支付更加便利,以前出门一部手机解决所有,而现在连手机都不需要了,毕竟,手机支付还需要携带手机,打开二维码也需要时间和手机信号.刷脸支付将会替代手机,成为新的支付方式.某地从大型超市门口随机抽取50名顾客进行了调查,得到了如表列联表:
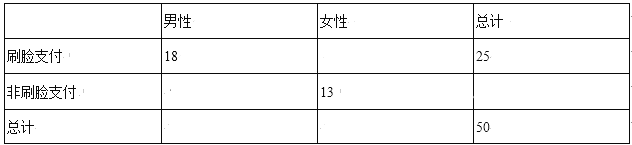
(1)请将上面的列联表补充完整,并判断是否有![]() 的把握认为使用刷脸支付与性别有关?
的把握认为使用刷脸支付与性别有关?
(2)从参加调查且使用刷脸支付的顾客中随机抽取2人参加抽奖活动,抽奖活动规则如下:“一等奖”中奖概率为0.25,奖品为10元购物券![]() 张(
张(![]() ,且
,且![]() ),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为
),“二等奖”中奖概率0.25,奖品为10元购物券两张,“三等奖”中奖概率0.5,奖品为10元购物券一张,每位顾客是否中奖相互独立,记参与抽奖的两位顾客中奖购物券金额总和为![]() 元,若要使
元,若要使![]() 的均值不低于50元,求
的均值不低于50元,求![]() 的最小值.
的最小值.
附: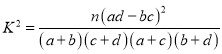 ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.如表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.
成绩优秀 | 成绩不够优秀 | 总计 | |
选修生涯规划课 | 15 | 10 | 25 |
不选修生涯规划课 | 6 | 19 | 25 |
总计 | 21 | 29 | 50 |
(1)根据列联表运用独立性检验的思想方法能否有99%的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
(2)现用分层抽样的方法在选修生涯规划课的成绩优秀和成绩不够优秀的学生中随机抽取5名学生作为代表,从5名学生代表中再任选2名学生继续调查,求这2名学生成绩至少有1人优秀的概率.
参考附表:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
参考公式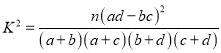 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,已知方程
,已知方程![]() (
(![]() 为常数)在
为常数)在![]() 上恰有三个根,分别为
上恰有三个根,分别为![]() ,下述四个结论:
,下述四个结论:
①当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;
;
②当![]() 时,
时,![]() 在
在![]() 上恰有2个极小值点和1个极大值点;
上恰有2个极小值点和1个极大值点;
③当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
④当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,且
,且![]()
其中正确的结论个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
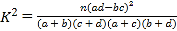 (其中
(其中![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com