
【题目】已知函数f(x)=2cos2x+ax2.
(1)当a=1时,求f(x)的导函数![]() 在
在![]() 上的零点个数;
上的零点个数;
(2)若关于x的不等式2cos(2sinx)+a2x2≤af(x)在(﹣∞,+∞)上恒成立,求实数a的取值范围.
【答案】(1)零点个数为3;(2)[1,+∞).
【解析】
(1)易得![]() =2(x﹣sin2x),再用导数法研究(0,
=2(x﹣sin2x),再用导数法研究(0,![]() )上的零点情况,然后结合
)上的零点情况,然后结合![]() 的奇偶性求解.
的奇偶性求解.
(2)令sinx=t∈[﹣1,1],转化为不等式cos2t≤a(1﹣t2)恒成立,再t=±1和﹣1<t<1分类讨论求解.
(1)易知![]() =2(x﹣sin2x),显然
=2(x﹣sin2x),显然![]() =0,
=0,
所以x=0是f′(x)的一个零点,
令g(x)=x﹣sin2x(0≤x![]() ),则
),则![]() =1﹣2cos2x=0时,x
=1﹣2cos2x=0时,x![]() ,
,
所以g(x)在(0,![]() )单调递减,在(
)单调递减,在(![]() ,
,![]() )单调递增,
)单调递增,
则g(x)的最小值为g(![]() )
)![]() 0,
0,
又g(0)=0,且g(![]() )
)![]() 0,
0,
所以g(x)在(0,![]() )上存在唯一零点x0∈(
)上存在唯一零点x0∈(![]() ,
,![]() ),
),
则![]() =2g(x)在(0,
=2g(x)在(0,![]() )上亦存在唯一零点,
)上亦存在唯一零点,
因为![]() 是奇函数,所以
是奇函数,所以![]() 在(
在(![]() ,0)上也存在唯一零点﹣x0,
,0)上也存在唯一零点﹣x0,
综上所述,当a=1时,f(x)的导函数![]() 在[
在[![]() ,
,![]() ]上的零点个数为3;
]上的零点个数为3;
(2)不等式2cos(2sinx)+a2x2≤af(x)恒成立,即不等式cos(2sinx)≤acos2x恒成立,
令sinx=t∈[﹣1,1],则等价于不等式cos2t≤a(1﹣t2)…(1)恒成立,
①若t2=1,即t=±1时,不等式(1)显然成立,此时a∈R,
②若﹣1<t<1时,不等式(1)等价于a![]() (2)
(2)
设h(t)![]() (﹣1<t<1),
(﹣1<t<1),
当0≤t<1时,![]()
 ,
,
令φ(t)=tcos2t﹣(1﹣t2)sin2t(0≤t<1,
则![]() =(2t2﹣1)cos2t(0≤t<1),
=(2t2﹣1)cos2t(0≤t<1),
已知 =0,
=0,![]() =0,且
=0,且![]() ,
,
则φ(t)在(0,![]() ),(
),(![]() ,1)上单调递减,在(
,1)上单调递减,在(![]() ,
,![]() )上单调地增,
)上单调地增,
又φ(0)=0,φ(![]() )=
)=![]() ﹣1<0,所以φ(t)<0在(0,1)上恒成立,
﹣1<0,所以φ(t)<0在(0,1)上恒成立,
所以h(t)在[0,1)上单调递减,则h(t)≤h(0)=1,
显然函数h(t)为偶函数,故函数h(t)在[﹣1,1]上的最大值为1,
因此a≥1,
综上所述,满足题意的实数a的取值范围为[1,+∞).


科目:高中数学 来源: 题型:
【题目】对某两名高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到折线图,下面是关于这两位同学的数学成绩分析.
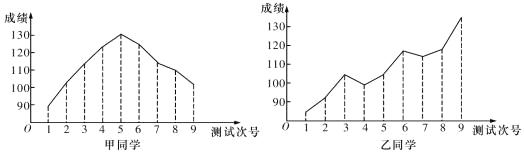
①甲同学的成绩折线图具有较好的对称性,故平均成绩为130分;
②根据甲同学成绩折线图提供的数据进行统计,估计该同学平均成绩在区间![]() 内;
内;
③乙同学的数学成绩与测试次号具有比较明显的线性相关性,且为正相关;
④乙同学连续九次测验成绩每一次均有明显进步.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C所对边的边长,且C=![]() ,a+b=λc(其中λ>1).
,a+b=λc(其中λ>1).
(1)若λ=![]() 时,证明:△ABC为直角三角形;
时,证明:△ABC为直角三角形;
(2)若![]() ·
·![]() =
=![]() λ2,且c=3,求λ的值.
λ2,且c=3,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二人进行一场比赛,该比赛采用三局两胜制,即先获得两局胜利者获得该场比赛胜利.在每一局比赛中,都不会出现平局,甲获胜的概率都为![]() .
.
(1)求甲在第一局失利的情况下,反败为胜的概率;
(2)若![]() ,比赛结束时,设甲获胜局数为
,比赛结束时,设甲获胜局数为![]() ,求其分布列和期望
,求其分布列和期望![]() ;
;
(3)若甲获得该场比赛胜利的概率大于甲每局获胜的概率,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1、F2分别为双曲线C:![]() (a>0,b>0)的左、右焦点,点M(x0,y0)(x0<0)为C的渐近线与圆x2+y2=a2的一个交点,O为坐标原点,若直线F1M与C的右支交于点N,且|MN|=|NF2|+|OF2|,则双曲线C的离心率为_____.
(a>0,b>0)的左、右焦点,点M(x0,y0)(x0<0)为C的渐近线与圆x2+y2=a2的一个交点,O为坐标原点,若直线F1M与C的右支交于点N,且|MN|=|NF2|+|OF2|,则双曲线C的离心率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线![]() 是过点
是过点![]() 的动直线,当
的动直线,当![]() 与圆
与圆![]() 相切时,同时也和抛物线
相切时,同时也和抛物线![]() 相切.
相切.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,与圆
,与圆![]() 交于不同的两点A、B,
交于不同的两点A、B,![]() 面积为
面积为![]() ,
,![]() 面积为
面积为![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》中给出了勾股定理的绝妙证明.如图是赵爽弦图及注文.弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成朱色及黄色,其面积称为朱实、黄实.由2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2.若图中勾股形的勾股比为![]() ,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:
,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:![]() ,
,![]() )
)
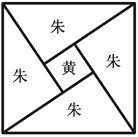
A.2B.4C.6D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com