Question

11．已知△ABC中，AC=$\sqrt{2}$，BC=$\sqrt{6}$，△ABC的面积为$\frac{{\sqrt{3}}}{2}$，若线段BA的延长线上存在点D，使∠BDC=$\frac{π}{4}$，则CD=$\sqrt{3}$．

Answer 1

分析 由已知利用三角形面积公式可求sin∠ACB=$\frac{1}{2}$，从而可求∠ACB=$\frac{π}{6}$，在△ABC中，由余弦定理可得AB，进而可求∠B，在△BCD中，由正弦定理可得CD的值．

解答 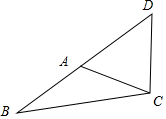解：∵AC=$\sqrt{2}$，BC=$\sqrt{6}$，△ABC的面积为$\frac{{\sqrt{3}}}{2}$=$\frac{1}{2}$AC•BC•sin∠ACB=$\frac{1}{2}×\sqrt{2}×\sqrt{6}×$sin∠ACB，
∴sin∠ACB=$\frac{1}{2}$，
∴∠ACB=$\frac{π}{6}$，或$\frac{5π}{6}$，
∵若∠ACB=$\frac{5π}{6}$，∠BDC=$\frac{π}{4}$＜∠BAC，可得：∠BAC+∠ACB＞$\frac{π}{4}$+$\frac{5π}{6}$＞π，与三角形内角和定理矛盾，
∴∠ACB=$\frac{π}{6}$，
∴在△ABC中，由余弦定理可得：AB=$\sqrt{A{C}^{2}+B{C}^{2}-2AC•BC•cos∠ACB}$=$\sqrt{2+6-2×\sqrt{2}×\sqrt{6}×\frac{\sqrt{3}}{2}}$=$\sqrt{2}$，
∴∠B=$\frac{π}{6}$，
∴在△BCD中，由正弦定理可得：CD=$\frac{BC•sinB}{sin∠BDC}$=$\frac{\sqrt{6}×\frac{1}{2}}{\frac{\sqrt{2}}{2}}$=$\sqrt{3}$．
故答案为：$\sqrt{3}$．

点评 本题主要考查了三角形面积公式，余弦定理，正弦定理在解三角形中的应用，考查了转化思想和数形结合思想，求∠ACB的值是解题的关键，属于中档题．