练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．命题“若a＞2，则a＞1”及其逆命题、否命题、逆否命题这四个命题中，真命题的个数为（　　）
    A．1B．2C．3D．4

    分析 根据四种命题真假之间的关系进行判断即可．

    解答 解：若a＞2，则a＞1，成立，即原命题为真命题，则逆否命题也为真命题，
    逆命题为：若a＞1，则a＞2，为假命题．，当a=1.5时，满足a＞1，但a＞2不成立，
    则否命题为假命题，
    故真命题的个数为2个，
    故选：B．

    点评 本题主要考查四种命题真假关系的判断，根据逆否命题的等价性只需要判断两个命题即可，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

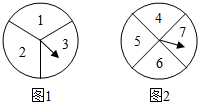    1．某校高一年级甲、已两班准备联合举行晚会，两班各派一人先进行转盘游戏，胜者获得一件奖品，负者表演一个节目．甲班的文娱委员利用分别标有数字1，2，3，4，5，6，7的两个转盘（如图所示），设计了一种游戏方案：两人同时各转动一个转盘一次，将转到的数字相加，和为偶数时甲班代表获胜，否则乙班代表获胜．
    （Ⅰ）根据这个游戏方案，转到的两数之和会出现哪些可能的情况？
    （Ⅱ）游戏方案对双方是否公平？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知命题p：“若直线a与平面α内两条直线垂直，则直线a与平面α垂直”，命题q：“存在两个相交平面垂直于同一条直线”，则下列命题中的真命题为（　　）
    A．p∧qB．p∨qC．￢p∨qD．p∧￢q

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．下列函数中，在其定义域内是偶函数为（　　）
    A．$f（x）=\frac{1}{x}$B．f（x）=2xC．f（x）=lgxD．f（x）=cosx

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．设f（x）=ax2+2x-2a在[-1，2）上是增函数，则a的取值范围是$[{-\frac{1}{2}，1}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知数列{an}满足an+1=an+1（n∈N*），且a1=1，则$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_{99}}{a_{100}}}}$=$\frac{99}{100}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

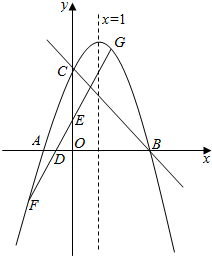    3．如图，对称轴为直线x=1的抛物线交x轴于点A、B，交y轴于点C（0，3），且S△ABC=6．
    （1）求此抛物线的解析式；
    （2）直线y=kx+1交x轴于点D，交y轴于点E，交抛物线于点F、G，在y轴上是否存在点P，使得以P、C、F、G为顶点的四边形是平行四边形？如果存在，求出k的值及点P的坐标；如果不存在，请说明理由；
    （3）在（2）的条件下，抛物线上是否存在点Q，使得OQ、AC、BC三条直线所围成的三角形与△DOE相似？如果存在，求出点Q的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=$\frac{ax+1}{x-3}$的反函数是f（x）本身，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．正项数列{an}的前n项和为Sn，且满足Sn2=（n2-n）Sn+n3
    （1）求an；
    （2）记数列{$\frac{1}{n{S}_{n}}$}的前n项和为Tn，用数学归纳法证明：Tn≤$\frac{5}{4}$-$\frac{1}{2n（n+1）}$对一切n∈N*都成立．

    查看答案和解析>>

    同步练习册答案