
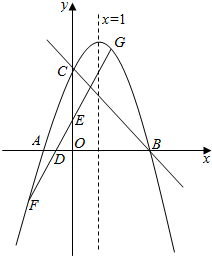
 如图,对称轴为直线x=1的抛物线交x轴于点A、B,交y轴于点C(0,3),且S△ABC=6.
如图,对称轴为直线x=1的抛物线交x轴于点A、B,交y轴于点C(0,3),且S△ABC=6.分析 (1)设A,B点坐标,设f(x)=a(x-x1)(x-x2),列出方程组解出x1,x2,a;
(2)将y=kx+1与二次函数解析式联立,求出F,G连点坐标的关系,假设存在点P,则E为FG和PC的中点,根据中点坐标公式列方程解出k和P点坐标;
(3)求出∠ACB,判断是否与Rt△ODE中的某个角相等,根据相似关系得出OQ与AC或BC的关系,列方程组求出Q坐标.
解答 解:(1)设A(x1,0),B(x2,0),抛物线解析式为f(x)=a(x-x1)(x-x2),则$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2}\\{a{x}_{1}{x}_{2}=3}\\{{x}_{2}-{x}_{1}=4}\end{array}\right.$,
解得a=-1,x1=-1,x2=3.
∴抛物线的解析式为f(x)=-(x+1)(x-3).
(2)假设在y轴上存在点P使得以P、C、F、G为顶点的四边形是平行四边形,
则E为平行四边形PFCG的对角线交点.
联立方程组$\left\{\begin{array}{l}{y=kx+1}\\{y=-(x+1)(x-3)}\end{array}\right.$得:x2+(k-2)x-2=0.
设F(x1,y1),G(x2,y2),则x1+x2=2-k,y1+y2=k(x1+x2)+2=-k2+2k+2,
∵E(0,1)是FG中点,∴$\left\{\begin{array}{l}{2-k=0}\\{-{k}^{2}+2k+2=2}\end{array}\right.$,解得k=2.
.∵E(0,1),C(0,3),∴P(0,-1).
(3)k=2时,D(-$\frac{1}{2}$,0),OD=$\frac{1}{2}$,OE=1,∴DE=$\frac{\sqrt{5}}{2}$,∴cos∠ODE=$\frac{\sqrt{5}}{5}$,cos∠OED=$\frac{2\sqrt{5}}{5}$.
∵AC=$\sqrt{10}$,BC=3$\sqrt{2}$,AB=4,∴cos∠ACB=$\frac{10+18-16}{2×\sqrt{10}×3\sqrt{2}}$=$\frac{\sqrt{5}}{5}$,∴∠ACB=∠ODE,
∴抛物线上存在点Q,使得OQ、AC、BC三条直线所围成的三角形与△DOE相似.
∵OD⊥OE,∴OQ⊥AC或OQ⊥BC.
直线AC方程为y=3x+3,直线BC方程为y=-x+3.
①若OQ⊥AC,则直线OQ方程为y=-$\frac{1}{3}x$,
联立方程组$\left\{\begin{array}{l}{y=-\frac{1}{3}x}\\{y=-(x+1)(x-3)}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{7+\sqrt{157}}{6}}\\{y=-\frac{7+\sqrt{157}}{18}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{7-\sqrt{157}}{6}}\\{y=-\frac{7-\sqrt{157}}{18}}\end{array}\right.$.
②若OQ⊥BC,则OQ方程为y=x.
联立方程组$\left\{\begin{array}{l}{y=x}\\{y=-(x+1)(x-3)}\end{array}\right.$,解得x=y=$\frac{1±\sqrt{13}}{2}$.
∴Q($\frac{7+\sqrt{157}}{6}$,-$\frac{7+\sqrt{157}}{18}$)或Q($\frac{7-\sqrt{157}}{6}$,-$\frac{7-\sqrt{157}}{18}$)或Q($\frac{1+\sqrt{13}}{2}$,$\frac{1+\sqrt{13}}{2}$)或Q($\frac{1-\sqrt{13}}{2}$,$\frac{1-\sqrt{13}}{2}$).
点评 本题考查了待定系数法求解析式,直线与抛物线的位置关系与综合计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
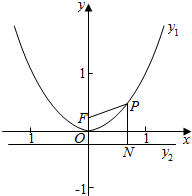 如图所示,在平面直角坐际系中有一抛物线y1=ax2,且抛物线经过点(2a-1,1),y轴上有一定点F,其坐标为(0,$\frac{1}{4}$),直线1的解析式为y2=-$\frac{1}{4}$,在抛物线上有一动点P,连接PF,并过点P作PN⊥直线1.
如图所示,在平面直角坐际系中有一抛物线y1=ax2,且抛物线经过点(2a-1,1),y轴上有一定点F,其坐标为(0,$\frac{1}{4}$),直线1的解析式为y2=-$\frac{1}{4}$,在抛物线上有一动点P,连接PF,并过点P作PN⊥直线1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com