
分析 由题意可得|ex-alnx+c-g(x)|对x∈(0,+∞)恒为常数,且不为0.令x=1求得常数.再由题意可得f(x)=ex-alnx+c在(2,3)上无极值点,运用导数和构造函数,转化为方程无实根,即可得到a的范围.
解答 解:由题意可得|ex-alnx+c-g(x)|对x∈(0,+∞)恒为常数,且不为0.
令x=1,可得|e-0+c-g(1)|=|e+c-e|=|c|>0.
由g(x)在区间(2,3)上的零点唯一,可得:
f(x)=ex-alnx+c在(2,3)上无极值点,
即有f′(x)=ex-$\frac{a}{x}$=$\frac{x{e}^{x}-a}{x}$,
则xex-a=0无实数解,
由y=xex,可得y′=(1+x)ex>0,在(2,3)成立,即有函数y递增,
可得y∈(2e2,3e3),
则a≥3e3,
故答案为:[3e3,+∞).
点评 本题考查新定义的理解和运用,考查函数零点问题的解法,考查转化思想的运用,注意运用导数,判断单调性,同时考查构造法的运用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
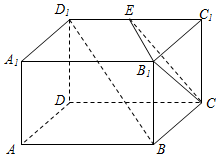 已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
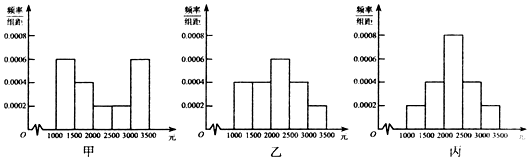
| A. | s1>s2>s3 | B. | s1>s3>s2 | C. | s3>s2>s1 | D. | s3>s1>s2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
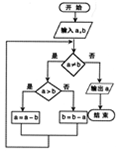 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
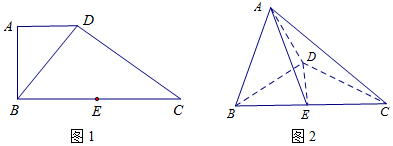
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com