
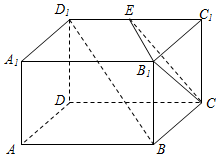
 已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.分析 (Ⅰ)连接BC1 交B1C于M,则直线ME即为平面ABD1 与平面B1EC的交线;
(Ⅱ)在长方体AC1 中,M为BC1 的中点,又E为D1C1的中点,由三角形中位线定理可得EM∥BD1,再由线面平行的判定可得BD1∥平面B1EC;
(Ⅲ)B到平面B1EC的距离d即为BD1中点到平面B1EC的距离,然后利用等积法即可求得BD1中点到平面B1EC的距离.
解答 (Ⅰ)解:连接BC1 交B1C于M,则直线ME即为平面ABD1 与平面B1EC的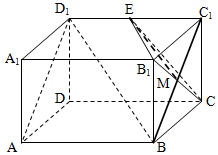 交线,如图所示;
交线,如图所示;
(Ⅱ)证明:由(Ⅰ),在长方体AC1 中,M为BC1 的中点,又E为D1C1的中点,
∴在△D1C1B中,EM是中位线,则EM∥BD1,
又EM?平面B1EC,BD1?平面B1EC,
∴BD1∥平面B1EC;
(Ⅲ)解:∵BD1∥平面B1EC,
∴B到平面B1EC的距离d即为BD1中点到平面B1EC的距离.
∵${V_{B-{B_1}CE}}={V_{E-{B_1}CB}}$,
∴$\frac{1}{3}S{\;}_{△{B_1}CE}•d=\frac{1}{3}S{\;}_{△{B_1}CB}•1$,
∵${B}_{1}C={B}_{1}E=\sqrt{5}$,EC=$\sqrt{2}$,
∴${S}_{△{B}_{1}EC}=\frac{1}{2}•\sqrt{2}•\sqrt{5-\frac{1}{2}}=\frac{3}{2}$,${S}_{{B}_{1}CB}=1$,
∴d=$\frac{2}{3}$.
点评 本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -20 | B. | 20 | C. | -160 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
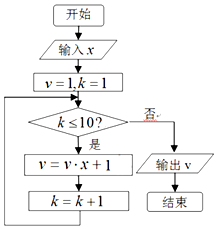 秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为 2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为 2,则输出v的值为( )| A. | 211-1 | B. | 211-2 | C. | 210-1 | D. | 210-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{9}{16}$ | B. | -1 | C. | $-\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com