
分析 (1)由题意可知:设椭圆的标准方程,c=$\frac{2\sqrt{2}}{3}$a,则利用椭圆的定义m+n=2a,勾股定理n2+(2c)2=m2,及向量数量积,即可求得a和b的值,求得椭圆方程;
(2)假设存在直线l,设出方程与椭圆方程联立,利用韦达定理,结合根的判别式,即可得到结论.
解答 解:(1)由题意可知:设题意的方程:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0),
e=$\frac{c}{a}$=$\frac{2\sqrt{2}}{3}$,则c=$\frac{2\sqrt{2}}{3}$a,设丨PF1丨=m,丨PF2丨=n,
则m+n=2a,
线段PF1为直径的圆经过F2,则PF2⊥F1F2,
则n2+(2c)2=m2,
9m•n×cos∠F1PF2=1,由9n2=1,n=$\frac{1}{3}$,解得:a=3,c=$\frac{2\sqrt{2}}{3}$,
则b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
∴椭圆标准方程:${x}^{2}+\frac{{y}^{2}}{9}=1$;
(2)假设存在直线l,依题意l交椭圆所得弦MN被x=-$\frac{1}{2}$平分,
∴直线l的斜率存在.
设直线l:y=kx+m,则
由 $\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+\frac{{y}^{2}}{9}=1}\end{array}\right.$消去y,整理得(k2+9)x2+2kmx+m2-9=0
∵l与椭圆交于不同的两点M,N,
∴△=4k2m2-4(k2+9)(m2-9)>0,即m2-k2-9<0①
设M(x1,y1),N(x2,y2),则x1+x2=-∴$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{km}{{k}^{2}+9}$=-$\frac{1}{2}$,∴m=$\frac{{k}^{2}+9}{2k}$②
把②代入①式中得($\frac{{k}^{2}+9}{2k}$)2-(k2+9)<0
∴k>$\sqrt{3}$或k<-$\sqrt{3}$,
∴直线l倾斜角α∈($\frac{π}{3}$,$\frac{π}{2}$)∪( $\frac{π}{2}$,$\frac{2π}{3}$).
点评 本题考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理,向量数量积,考查学生的计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 同意限定区域停车 | 不同意限定区域停车 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在$(0,\frac{π}{4})$上单调递减 | B. | f(x)在$(\frac{π}{8},\frac{3π}{8})$上单调递减 | ||
| C. | f(x)在$(0,\frac{π}{4})$上单调递增 | D. | f(x)在$(\frac{π}{8},\frac{3π}{8})$上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
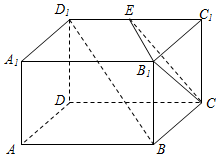 已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
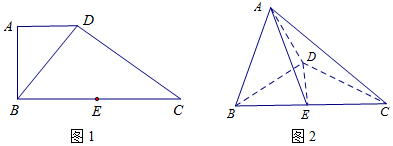
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com