
| A. | -20 | B. | 20 | C. | -160 | D. | 240 |
分析 利用定积分求出a的值,再利用二项式展开式的通项公式求出展开式的常数项.
解答 解:$a=\int_0^π{sinxdx}$=-cosx${|}_{0}^{π}$=-(cosπ-cos0)=2,
则${(a\sqrt{x}+\frac{1}{x})^6}$=${(2\sqrt{x}+\frac{1}{x})}^{6}$展开式的通项公式为:
Tr+1=${C}_{6}^{r}$•${(2\sqrt{x})}^{6-r}$•${(\frac{1}{x})}^{r}$
=26-r•${x}^{3-\frac{3}{2}r}$•${C}_{6}^{r}$,
令3-$\frac{3}{2}$r=0得:r=2.
∴展开式中的常数项为24•${C}_{6}^{2}$=240.
故选:D.
点评 本题考查了定积分与二项式展开式的通项公式应用问题,是基础题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在$(0,\frac{π}{4})$上单调递减 | B. | f(x)在$(\frac{π}{8},\frac{3π}{8})$上单调递减 | ||
| C. | f(x)在$(0,\frac{π}{4})$上单调递增 | D. | f(x)在$(\frac{π}{8},\frac{3π}{8})$上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
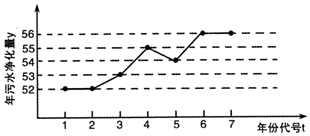
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
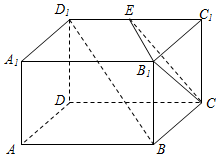 已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
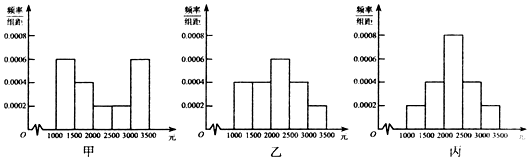
| A. | s1>s2>s3 | B. | s1>s3>s2 | C. | s3>s2>s1 | D. | s3>s1>s2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com