
���� ������ƽ�����������������㼰���Ǻ����еĺ�ȱ任Ӧ�ÿɵú�������ʽΪ��f��x��=2sin��2x+$\frac{��}{6}$��+1����2k��-$\frac{��}{2}$��2x+$\frac{��}{6}$��2k��+$\frac{��}{2}$��k��Z���ɽ��f��x���ĵ����������䣮
������f��$\frac{A}{2}$��=3�ɵ�sin��A+$\frac{��}{6}$��=1�����A��Χ����A��C=$\frac{2��}{3}$-B����sinBsinC=$\frac{3}{4}$�������Ǻ����еĺ�ȱ任Ӧ�ÿɵ�sin��2B-$\frac{��}{6}$��=1������-$\frac{��}{6}$��2B-$\frac{��}{6}$$��\frac{7��}{6}$���ɵ�2B-$\frac{��}{6}$=$\frac{��}{2}$���Ӷ��ý�B��C��ֵ���ɵá�ABCΪ�ȱ������Σ�
��� ����������Ϊ12�֣�
�⣺������$\overrightarrow{m}$��$\overrightarrow{n}$���ɵ�$\overrightarrow{m}$•$\overrightarrow{n}$=0���ɵ�2cos2x+2$\sqrt{3}$sinxcosx-y=0�����У�f��x��=2sin��2x+$\frac{��}{6}$��+1��
��2k��-$\frac{��}{2}$��2x+$\frac{��}{6}$��2k��+$\frac{��}{2}$��k��Z���ɵ�f��x���ĵ�����������Ϊ��[k$��-\frac{��}{3}$��k$��+\frac{��}{6}$]��k��Z��6��
����f��$\frac{A}{2}$��=3��
��2sin��A+$\frac{��}{6}$��+1=3����sin��A+$\frac{��}{6}$��=1��
�֡�0��A���У������A=$\frac{��}{3}$��
��A+B+C=��
��C=$\frac{2��}{3}$-B��
��sinBsinC=$\frac{3}{4}$��
⇒sinBsin��$\frac{2��}{3}$-B��=$\frac{3}{4}$��
⇒sinB��sin$\frac{2��}{3}$cosB-cos$\frac{2��}{3}$sinB��=$\frac{3}{4}$��
⇒$\frac{\sqrt{3}}{2}sinBcos\\;B+\frac{1}{2}si{n}^{2}B=\frac{3}{4}$B$+\frac{1}{2}si{n}^{2}B=\frac{3}{4}$��
⇒$\frac{\sqrt{3}}{4}$sin2B+$\frac{1}{4}��1-cos2B��=\frac{3}{4}$��
⇒$\frac{\sqrt{3}}{2}$sin2B-$\frac{1}{2}$cos2B=1
⇒sin��2B-$\frac{��}{6}$��=1
�֡�-$\frac{��}{6}$��2B-$\frac{��}{6}$$��\frac{7��}{6}$��
��2B-$\frac{��}{6}$=$\frac{��}{2}$��
��B=$\frac{��}{3}$��C=$\frac{��}{3}$����ABCΪ�ȱ������Ρ�12��
���� ������Ҫ������ƽ�����������������㣬���Ǻ����еĺ�ȱ任Ӧ�ã����Һ�����ͼ������ʣ����ڻ���֪ʶ�Ŀ��飮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 8 | B�� | 9 | C�� | 10 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
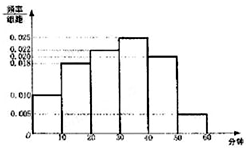 ���Ӵ�ý��˾Ϊ���˽�ij�������ӹ��ڶ�ij��������Ŀ����������������ȡ��100�����ڽ��е��飬����Ů����55���������Ǹ��ݵ��������ƵĹ����վ��տ���������Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ��
���Ӵ�ý��˾Ϊ���˽�ij�������ӹ��ڶ�ij��������Ŀ����������������ȡ��100�����ڽ��е��飬����Ů����55���������Ǹ��ݵ��������ƵĹ����վ��տ���������Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ�� | �������� | ������ | �ϼ� | |
| �� | |||
| Ů | |||
| �ϼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 0 | C�� | -1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��0��1} | B�� | {0��1} | C�� | {0} | D�� | {-1��0} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 34�� | B�� | 72�� | C�� | 64�� | D�� | 36�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com