练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，角A，B，C所对的边长分别为a，b，c．若C＝120°，c＝a，则(    )

    A．a>b

    B．a<b

    C．a＝b

    D．a与b的大小关系不能确定

     

    A

    【解析】方法一：由余弦定理得2a2＝a2＋b2－2abcos120°，

    ∴b2＋ab－a2＝0，

    即()2＋－1＝0＝<1，故b<a．

    方法二：由余弦定理得2a2＝a2＋b2－2abcos120°，

    ∴b2＋ab－a2＝0，

    即b2＝a2－ab＝a(a－b)>0，∴a>b．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014高考名师推荐数学理科利用导数求最值和极值（解析版） 题型：解答题

    已知函数其中a是实数．设，为该函数图象上的两点，且．

    （1）指出函数f(x)的单调区间;

    （2）若函数f(x)的图象在点A，B处的切线互相垂直，且，求的最小值;

    （3）若函数f(x)的图象在点A，B处的切线重合，求a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科函数与方程（解析版） 题型：选择题

    若函数有极值点，且，则关于x的方程的不同实根个数是( )

    A．3 B．4 C．5 D．6

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科几何概型（解析版） 题型：选择题

    如图，在圆心角为直角的扇形OAB中，分别以OA，OB为直径作两个半圆． 在扇形OAB

    内随机取一点，则此点取自阴影部分的概率是（ ）

    A． B． C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科全称量词与存在性量词（解析版） 题型：选择题

    已知命题p：“?x∈R，?m∈R，使4x＋2x·m＋1＝0”．若命题p为真命题，则实数m的取值范围是

    A. (－∞，－2]

    B. [2,+∞)

    C. (－∞，－2)

    D. (2,+∞)

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科余弦定理（解析版） 题型：选择题

    △ABC的三内角A，B，C所对边长分别是a，b，c，设向量m＝(a＋b，sinC)，n＝(a＋c，sinB－sinA)，若m∥n，则角B的大小为（    ）

    A．30°

    B．60°

    C．120°

    D．150°

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科二项式定理与性质（解析版） 题型：选择题

    1．若，则的值为（ ）

    A．1 B．－1 C．0 D．2

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科两角和与差的三角函数、倍角公式（解析版） 题型：选择题

    设当x=θ时，函数f(x)＝sinx－2cosx取得最大值，则cosθ= (     )

    A.-

    B.

    C.-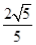

    D.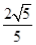

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题

    如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB.

    （1）求证：CE⊥平面PAD；

    （2）若PA=AB=1，AD=3，CD=，∠CDA=45°，求四棱锥P-ABCD的体积.

     

     

    查看答案和解析>>

    同步练习册答案