
已知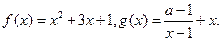
(I)a=2时,求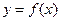 和
和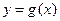 的公共点个数;
的公共点个数;
(II)a为何值时,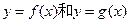 的公共点个数恰为两个。
的公共点个数恰为两个。
科目:高中数学 来源: 题型:解答题
(本题满分13分)
某市旅游部门开发一种旅游纪念品,每件产品的成本是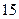 元,销售价是
元,销售价是 元,月平均销售
元,月平均销售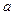 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
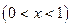 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为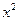 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是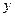 (元).
(元).
(1)写出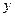 与
与 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=()x,
函数y=f-1(x)是函数y=f(x)的反函数.
(1)若函数y=f-1(mx2+mx+1)的定义域为R,求实数m的取值范围;
(2)当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值g(a);
(3)是否存在实数m>n>3,使得g(x)的定义域为[n,m],值域为[n2,m2]?若存在,求出m、n的值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
设 为奇函数,
为奇函数, a为常数。
a为常数。
(1) 求a的值;
(2) 证明 在区间
在区间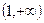 上为增函数;
上为增函数;
(3) 若对于区间 上的每一个
上的每一个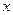 的值,不等式
的值,不等式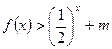 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
已知函数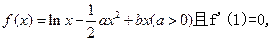
(I)试用含a的式子表示b,并求函数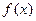 的单调区间;
的单调区间;
(II)已知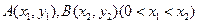 为函数
为函数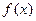 图象上不同两点,
图象上不同两点,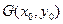 为AB的中点,记A、B两点连线的斜率为k,证明:
为AB的中点,记A、B两点连线的斜率为k,证明: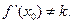
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com