
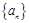 满足:
满足: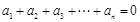 且
且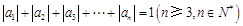 ,则称数列
,则称数列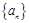 为
为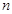 阶“归化数列”.
阶“归化数列”.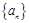 是等比数列,写出该数列的各项;
是等比数列,写出该数列的各项;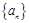 是等差数列,求该数列的通项公式;
是等差数列,求该数列的通项公式;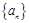 为n阶“归化数列”,求证:
为n阶“归化数列”,求证: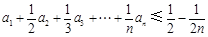 .
.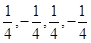 或
或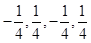 ;(2)
;(2) 或
或 ;(3)证明见解析.
;(3)证明见解析.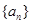 是4阶“归化数列”,则有
是4阶“归化数列”,则有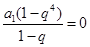 ,这样
,这样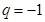 ,于是
,于是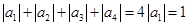 ,从而
,从而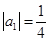 ,
,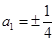 ,以后各项依次可写出;(2)等差数列
,以后各项依次可写出;(2)等差数列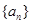 是11阶“归化数列”,则
是11阶“归化数列”,则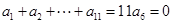 ,
,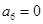 ,这样有
,这样有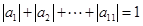 ,知当
,知当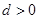 时,
时,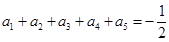 ,当
,当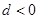 时,
时,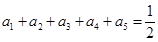 ,由此可得
,由此可得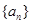 的通项公式分别为
的通项公式分别为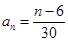 或
或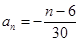 ;(3)对
;(3)对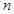 阶“归化数列”,从已知上我们只能知道在
阶“归化数列”,从已知上我们只能知道在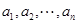 中有正有负,因此为了求
中有正有负,因此为了求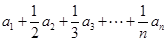 ,我们可以设
,我们可以设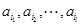 是正的,
是正的,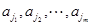 是负的,这样
是负的,这样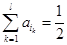 ,
,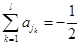 ,
,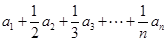
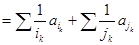
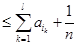
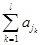
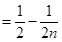
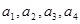 成公比为
成公比为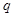 的等比数列,显然
的等比数列,显然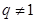 ,则由
,则由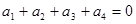 ,
,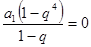 ,解得
,解得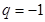 ,由
,由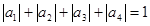 得
得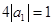 ,解得
,解得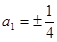 ,
,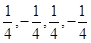 或
或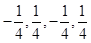 为所求四阶“归化数列”; 4分
为所求四阶“归化数列”; 4分 的公差为
的公差为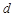 ,由
,由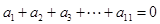 ,
,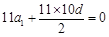 ,所以
,所以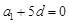 ,即
,即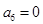 , 6分
, 6分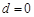 时,与归化数列的条件相矛盾,
时,与归化数列的条件相矛盾,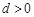 时,由
时,由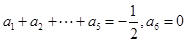 ,所以
,所以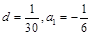 ,
,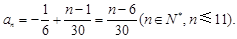 8分
8分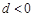 时,由
时,由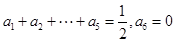 ,所以
,所以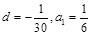 ,
,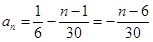 (n∈N*,n≤11),
(n∈N*,n≤11),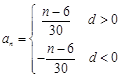 (n∈N*,n≤11), 10分
(n∈N*,n≤11), 10分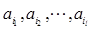 为诸ai中所有大于0的数,
为诸ai中所有大于0的数,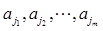 为诸ai中所有小于0的数.
为诸ai中所有小于0的数.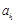 +
+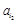 + +
+ +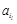 =
=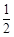 ,Y=
,Y= 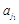 +
+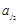 + +
+ +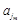 =-
=-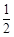 .
.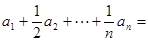
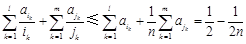 . 16分
. 16分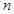 项和公式,不等式的放缩法.
项和公式,不等式的放缩法.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:不详 题型:解答题
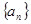 的各项均为正数,且
的各项均为正数,且
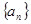 的通项公式;
的通项公式;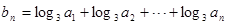 ,求数列
,求数列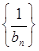 的前n项和
的前n项和 ;
;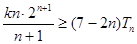 恒成立的实数
恒成立的实数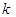 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com