
(本小题满分10分)选修4-5:不等式选讲
设关于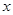 的不等式
的不等式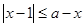 .
.
(I) 当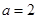 ,解上述不等式。
,解上述不等式。
(II)若上述关于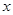 的不等式有解,求实数
的不等式有解,求实数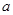 的取值范围。
的取值范围。
(I) 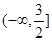 ;(II)
;(II) 。
。
解析试题分析:(I) 当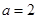 ,上述不等式为
,上述不等式为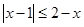 ,等价于
,等价于
①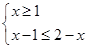 或 ②
或 ②
由得① ,由得②
,由得②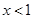 ;所以不等式解集为
;所以不等式解集为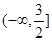 。 …………5分
。 …………5分
(II)解法一:
当x≥1时,不等式化为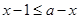 ,即x≤
,即x≤ .
.
这时不等式有解当且仅当1≤ ,即a≥1.
,即a≥1.
当x<1时,不等式化为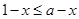 ,即1≤a,这时不等式有解当且仅当a≥1.
,即1≤a,这时不等式有解当且仅当a≥1.
综上所述,关于x的不等式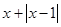 ≤a有解,
≤a有解,
则实数a的取值范围是 . ………10分
. ………10分
解法二:不等式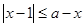 等价于
等价于
设 ,则
,则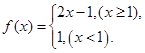
易知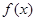 的最小值为1。
的最小值为1。
关于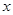 的不等式
的不等式 有解,即
有解,即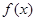 ≤a有解,所以a≥1。 ……10分
≤a有解,所以a≥1。 ……10分
考点:含绝对值不等式的解法。
点评:解含绝对值不等式的主要方法:一是利用绝对值不等式的几何意义来求解,体现了数形结合的思想;二是利用“零点分段法”进行分段讨论,去掉绝对值符号,从而求解,体现了分类讨论的思想。三是通过构造函数,利用函数的图像来求解,体现了函数与方程的思想。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知(x+1)n=a0+a1(x﹣1)+a2(x﹣1)+a3(x﹣1)3+…+an(x﹣1)n,(其中n∈N*)
(1)求a0及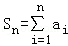 ;
;
(2)试比较Sn与(n﹣2)2n+2n2的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知集合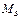 是满足下列性质的函数
是满足下列性质的函数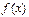 的全体:对于定义域B中的任何两个自变量
的全体:对于定义域B中的任何两个自变量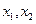 ,都有
,都有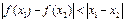 。(1)当B=R时,
。(1)当B=R时,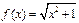 是否属于
是否属于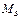 ?为什么?(2)当B=
?为什么?(2)当B=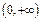 时,
时,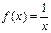 是否属于
是否属于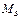 ,若属于请给予证明;若
,若属于请给予证明;若
不属于说明理由,并说明是否存在一个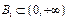 使
使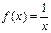 属于
属于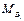 ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com