
分析 (1)an+1=2an-n+1,可得an+1-(n+1)=2(an-n),即bn+1=2bn.即可证明.
(2)由(1)可得:bn=an-n=2n.可得${c_n}=\frac{{{a_n}-n}}{{({{b_n}+1})({{b_{n+1}}+1})}}$=$\frac{{2}^{n}}{({2}^{n}+1)({2}^{n+1}+1)}$=$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$.利用裂项求和方法、数列的单调性即可证明.
解答 证明:(1)∵an+1=2an-n+1,∴an+1-(n+1)=2(an-n),即bn+1=2bn.
∵a1-1=2,∴{an-n}是以2为首项,2为公比的等比数列.
(2)由(1)可得:bn=an-n=2n.
∴${c_n}=\frac{{{a_n}-n}}{{({{b_n}+1})({{b_{n+1}}+1})}}$=$\frac{{2}^{n}}{({2}^{n}+1)({2}^{n+1}+1)}$=$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$.
∴Tn=$(\frac{1}{2+1}-\frac{1}{{2}^{2}+1})$+$(\frac{1}{{2}^{2}+1}-\frac{1}{{2}^{3}+1})$+…+$(\frac{1}{{2}^{n}+1}-\frac{1}{{2}^{n+1}+1})$
=$\frac{1}{3}-\frac{1}{{2}^{n+1}+1}$$<\frac{1}{3}$.
点评 本题考查了数列递推关系、等比数列的定义通项公式、裂项求和方法,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 四棱锥P-ABCD,侧面PCD为边长为2的正三角形,底面ABCD为对角线互相垂直的等腰梯形,M为AD的中点,$PO=\sqrt{2}$.
四棱锥P-ABCD,侧面PCD为边长为2的正三角形,底面ABCD为对角线互相垂直的等腰梯形,M为AD的中点,$PO=\sqrt{2}$. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
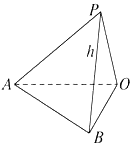 如图所示,在地面上有一旗杆OP,为测得它的高度h,在地面上取一线段AB,
如图所示,在地面上有一旗杆OP,为测得它的高度h,在地面上取一线段AB,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{3-2\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 12 | C. | 18 | D. | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com